Reducing SDP to QE problems

In this section we consider the method to solve BMI problems by using QE [2]. This method is applicable to not only BMI but also general matrix inequality (Polynomial Matrix Inequality; PMI). Here we denote a polynomial matrix inequality by $M(X) >_d (or \geq_d) 0$ , where $X=\{x_1,\cdots,x_n \}$ and we use $>_d (\geq_d)$ for definiteness of matrices in order to distinguish ordinary inequality sign.

Determining (semi)definiteness for a real symmetric matrix is achieved without computing eigenvalues by using the following well-known as Sylvester's theorem; For a matrix $M \in$ R $^{n\times n}$, we denote by

$$M \left ( \begin{array}{c} i_1 \ i_2 \ \cdots \ i_r \\ j_1 \ j_2 \ \cdots \ j_r \end{array}\right )$$

the $r \times r$ submatrix of M which consists of (i_k,j_l)-entries of M, where $1 \leq i_1 < i_2 < \cdots < i_r \leq n$ and $1 \leq j_1 < j_2 < \cdots < j_r \leq n$.

Theorem 1 (Sylvester's criterion)   Let $M=(a_{ij}) \in$ C $^{n\times n}$ be a Hermitian matrix. Then

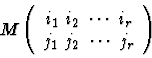
(i) M is positive semi-definite if and only if all principal minors of M are non negative i.e.

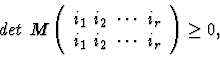$$det \ M \left ( \begin{array}{c} i_1 \ i_2 \ \cdots \ i_r \\ i_1 \ i_2 \ \cdots \ i_r \end{array}\right ) \geq 0,$$ (6)

for $1 \leq i_1 < i_2 < \cdots < i_r \leq n, \ r=1,2,\cdots,n.$

(ii) M is positive definite if and only if all leading principal minors of M are positive i.e.

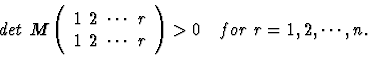$$det \ M \left ( \begin{array}{c} 1 \ 2 \ \cdots \ r \\ 1 \ 2... ...cdots \ r \end{array}\right ) > 0 \ \ \ for \ r=1,2,\cdots,n.$$ (7)

This is the key to reduce SDP problems to QE problems. By Theorem 1 (i), $M(x) \geq_d 0$ can be reduced to the formula which is the conjunction of $2^n-1 ( \equiv \sum_{r=1}^n \ _nC_r)$ inequalities.

Remark 1   By this theorem, Positive-Definite Programming can be also resolved in the same manner as SDP problems if we use (ii).