Approximate factorization of multivariate polynomial is that, given
a polynomial
F in
![${\mathbf C}[x,y,\ldots,z]$](img3.gif)
,
we determine polynomials
G,
H
and
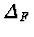
in
![${\mathbf C}[x,y,\ldots,z]$](img3.gif)
satisfying
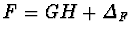
,
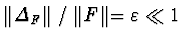
,
where
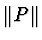
denotes a suitably
defined
norm of polynomial
P.
For approximate factorization, we need a completely different
algorithm from those for exact factorization. In 1991,
Sasaki et al. presented an algorithm of approximate factorization.
The algorithm determines irreducible factors by handling
the combinations of roots of the form
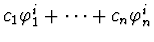
,
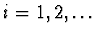
,
where
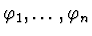
are the power-series roots of a given polynomial
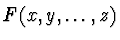
and
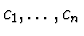
are numbers.
The algorithm was analyzed by Sasaki et al. in 1992, but it was
incomplete in that the truncation degree of power-series roots was
not shown. In this paper, we give a sufficient condition to
truncate the power-series, improve the algorithm in several points,
and show that the algorithm works in polynomial-time w.r.t.
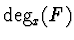
and
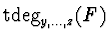
.
![]() and Tateaki Sasaki
and Tateaki Sasaki
![]()
![]() Doctoral Program of Mathematics
Doctoral Program of Mathematics ![]() Institute of Mathematics
Institute of Mathematics