Full paper in compressed Postscript *.ps.gz
The paper describes the algorithms for investigation of stability of mechanical systems. These algorithms are implemented with the aid of the computer algebra system (CAS) in the software package "STABILITY". Package investigates stability and stabilization of mechanical systems in both pure symbolic and numerical-symbolic forms [1].
Let's consider the stability task for trivial solution of matrix
differential equation
This presentation is possible for differential equations of perturbed
movement in the neighborhood of stationary motion or invariant set of
stationary motions. Algorithm to reduce equations to form (1) and
algorithm to classify nonlinear forces
![]() suitable for
implementation with CAS are described in [2]. There are three specific
groups of the tasks.
suitable for
implementation with CAS are described in [2]. There are three specific
groups of the tasks.
Investigation of stability in the first approximation.
The question of asymptotical stability or instability can be investigated
by studying of the first approximation equations
( when in eq. (1)
![]() ) ,
if we'd use classic Lyapunov's theorems.
) ,
if we'd use classic Lyapunov's theorems.
Step 1. Construct characteristic equation of the system (1):
Step 2. Analyze the structure of the polynomial (2).
Step 2.1. If polynomial (2) contains all powers of ![]() ,
then we construct the Hurwitz matrix and write out all Routh-Hurwitz
conditions and their analogies.
It gives us necessary and sufficient conditions that all roots of (2)
have negative real parts. If these conditions are met, then the motion
is asymptotically stable, independently from nonlinearities
,
then we construct the Hurwitz matrix and write out all Routh-Hurwitz
conditions and their analogies.
It gives us necessary and sufficient conditions that all roots of (2)
have negative real parts. If these conditions are met, then the motion
is asymptotically stable, independently from nonlinearities
![]() .
These condition comprise the system of algebraic inequalities of system
parameters (matrix elements of equation (1), amplification coefficients
in linear controlling forces, etc). Inequalities are written out in either
symbolic or numerical-symbolic form.
A description of some algorithms for solving the systems
of algebraic inequalities is given in [2].
The software implementation of these algorithms allows us to solve following
tasks:
.
These condition comprise the system of algebraic inequalities of system
parameters (matrix elements of equation (1), amplification coefficients
in linear controlling forces, etc). Inequalities are written out in either
symbolic or numerical-symbolic form.
A description of some algorithms for solving the systems
of algebraic inequalities is given in [2].
The software implementation of these algorithms allows us to solve following
tasks:
a). Finding the domains, which satisfy the inequalities
of one-parameter polynomials with numerical coefficients
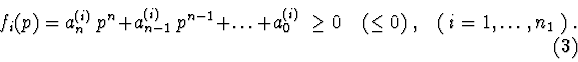
b). Search and graphical constructing of two-dimensional
domains corresponding to a system of algebraic inequalities
where ![]() is the parameter reckoned on the abscissa axis,
and
is the parameter reckoned on the abscissa axis,
and ![]() is the parameter reckoned on the axis of ordinates.
The boundaries of variation of the parameters
is the parameter reckoned on the axis of ordinates.
The boundaries of variation of the parameters ![]() and
and ![]() for constructing 2D - domains are determined as the solutions of problem (a).
for constructing 2D - domains are determined as the solutions of problem (a).
Step 2.2. If in polynomial (2) some powers of ![]() are absent,
we must conclude that the system is structurally unstable.
are absent,
we must conclude that the system is structurally unstable.
Step 2.2.1. Let in polynomial (2) all coefficients be
![]() This is always true if in linear part of the system are present
(i) positionary forces (potential or non-conservative) or
(ii) together with potential forces are present gyroscopic ones.
Stability of such a system is possible only in a critical case when
all roots of characteristic polynomial are imaginary or(and) zero.
Let's substitute
This is always true if in linear part of the system are present
(i) positionary forces (potential or non-conservative) or
(ii) together with potential forces are present gyroscopic ones.
Stability of such a system is possible only in a critical case when
all roots of characteristic polynomial are imaginary or(and) zero.
Let's substitute
![]() in equation (2). For resulting
equation of power n let's write out the conditions when all
roots of the polynomial are negative (different) real numbers [3].
This way we get the stability conditions of linear system and necessary
conditions of stability of nonlinear system (1).
in equation (2). For resulting
equation of power n let's write out the conditions when all
roots of the polynomial are negative (different) real numbers [3].
This way we get the stability conditions of linear system and necessary
conditions of stability of nonlinear system (1).
Direct calculation of characteristic equation (2) requires
us to calculate large determinants. Thus it's preferable to use some methods
of decomposition.
Let's suppose that lagrangian ![]() of the system allows presentation in the
form
of the system allows presentation in the
form
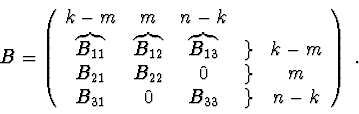
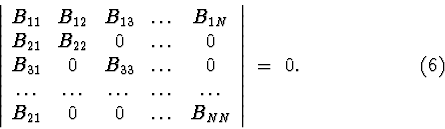
Investigation of stability by second Lyapunov's method. Sufficient conditions of stability, asymptotic stability or instability can be obtained by using theorems of second Lyapunov's method.
In critical cases , only the Lyapunov's second method is used. But then there arises the problem of the proximity of sufficient stability conditions to necessary conditions, i.e. of a "good" choice of the Lyapunov function . As investigations show, in critical cases sufficiently soft stability conditions are obtained when the first integral of the differential equations of motion is taken as the Lyapunov function.
Definition. The relation
![]() is said to be the differential consequence of equations (1) if it holds
for all solutions of the system.
is said to be the differential consequence of equations (1) if it holds
for all solutions of the system.
In the theorems of the Lyapunov's second method, we shall use
differential
consequences of equations (1). One of the algorithms for constructing
differential consequences is described in [1] and involves the
following procedure : we multiply (1) on the left by matrices of the form
![]() and
transform the final expressions by selecting the symmetric parts.
The matrices
and
transform the final expressions by selecting the symmetric parts.
The matrices
![]() are equal to those of the initial equation or their
combinations.
are equal to those of the initial equation or their
combinations.
Example 1. Let
![]() ,
and
,
and
![]() . After selecting the full derivative, we
obtain three consequences.
We combine them into one bunch :
. After selecting the full derivative, we
obtain three consequences.
We combine them into one bunch :
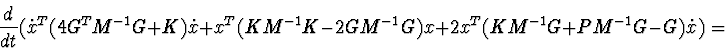
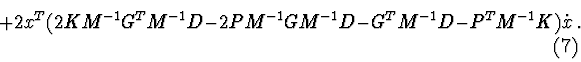
Let's define the function ![]() :
:
here
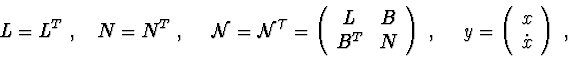
Let's calculate derivative of function (8) for equation (1):
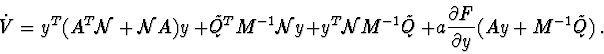
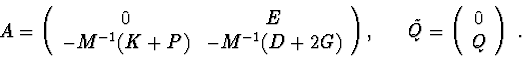
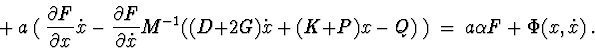
Variant 1. ![]() is given definitively positive (negative) matrix.
From classical theorems it is known that if at least one of
characteristic equation (2) roots has positive real part,
for equation (9) there always exist such
is given definitively positive (negative) matrix.
From classical theorems it is known that if at least one of
characteristic equation (2) roots has positive real part,
for equation (9) there always exist such
![]() and
and
![]() that
that
![]() isn't
sign-definite with sign, opposite to sign of
isn't
sign-definite with sign, opposite to sign of ![]() Vice versa, if for equation (9) with
Vice versa, if for equation (9) with
![]() are found
are found
![]() and
and
![]() and
and
![]() is not definitively negative, then trivial solution
of equation (1) is not stable and some roots
is not definitively negative, then trivial solution
of equation (1) is not stable and some roots
![]() of eq. (2)
have positive real part.
of eq. (2)
have positive real part.
Variant 2.
![]() is given definitively negative (positive) matrix.
It is known that if all roots of characteristic equation (2) of system (1)
have negative real parts, then in (9) there is only one solution for
is given definitively negative (positive) matrix.
It is known that if all roots of characteristic equation (2) of system (1)
have negative real parts, then in (9) there is only one solution for
![]() . In these conditions obtained matrix is definitively positive
(negative). Vice versa, if with given
. In these conditions obtained matrix is definitively positive
(negative). Vice versa, if with given
![]() it's found solution
it's found solution ![]() of equation (9) and
of equation (9) and
![]() , then zero solution of equation (1) is
asymptotically stable and all
, then zero solution of equation (1) is
asymptotically stable and all ![]() of equation (2) have negative
real parts.
of equation (2) have negative
real parts.
If roots ![]() of equation (2) are such that
of equation (2) are such that
![]() and
some of them have positive real part, then equation (9) have single solution
and
some of them have positive real part, then equation (9) have single solution
![]() and
and
![]() is not definitively positive (negative).
Zero solution of system (1) is unstable.
is not definitively positive (negative).
Zero solution of system (1) is unstable.
Variant 3. ![]() Then equation (9) is equivalent to equation [4] :
Then equation (9) is equivalent to equation [4] :
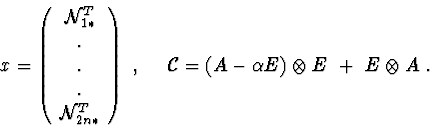
Let's write out equation (10) in the form :
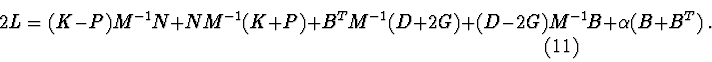
Let ![]() Then matrix
Then matrix ![]() is a solution of over-defined system :
is a solution of over-defined system :
From first equation it follows that
![]() are eigenvalues
of matrix
are eigenvalues
of matrix
![]() Second equation always have set of
nontrivial solutions. From second and third equations
if follows the condition
Second equation always have set of
nontrivial solutions. From second and third equations
if follows the condition
![]() when system (1) is critical.
Then third equation (12) has nontrivial solution. The solution of system (12)
can be used as Lyapunov function
when system (1) is critical.
Then third equation (12) has nontrivial solution. The solution of system (12)
can be used as Lyapunov function
![]() because if
because if ![]() satisfies system (12) then
satisfies system (12) then ![]()
Example 2. Consider a system with two degrees of freedom :
![]() System (12) has the form :
System (12) has the form :
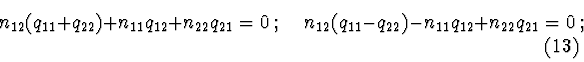
Solution 1. Let
![]() When
When
![]() system (13)
allows the solution :
system (13)
allows the solution :
![]() Consequently (8) has the form :
Consequently (8) has the form :
Solution 2. Let
![]() Then from system (13) we obtain :
Then from system (13) we obtain :
![]() ,
,
![]() ,
,
![]() ( in the system are present dissipative, gyroscopic, potential and
nonconservative positional forces),
( in the system are present dissipative, gyroscopic, potential and
nonconservative positional forces),
![]() Lyapunov function has the form
Lyapunov function has the form
![]() . For eqs. (13)
. For eqs. (13)
![]() When
When
![]() and
and
![]() trivial solution is asymptotically stable
with respect to
trivial solution is asymptotically stable
with respect to
![]() When
When
![]() trivial solution is
unstable.
trivial solution is
unstable. ![]()
Variant 4.
![]() Then we obtain two groups of
conditions when equation (1) has first integral of form (8) :
Then we obtain two groups of
conditions when equation (1) has first integral of form (8) :
a)
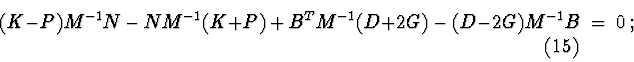
b)
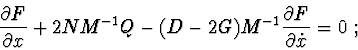
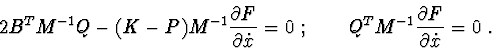
Equations of group (b) are used to build
![]() if it exists or
to find such
if it exists or
to find such ![]() that eq. (8) is an integral.
Function
that eq. (8) is an integral.
Function
![]() must fulfill the conditions:
must fulfill the conditions:
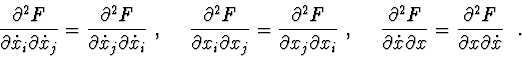
System (a) (14)-(16) always has trivial solution
![]() .
It is a system of uniform linear equations and can have (i) only trivial
solution or (ii) set of solutions.
If there exists nontrivial solution
.
It is a system of uniform linear equations and can have (i) only trivial
solution or (ii) set of solutions.
If there exists nontrivial solution
![]() then
then
![]() ,
,
![]() ( where
( where
![]() are matrices commutative with
are matrices commutative with
![]() ) are solutions too.
Existence conditions for nontrivial solution give us limitations on
matrices of original system.
) are solutions too.
Existence conditions for nontrivial solution give us limitations on
matrices of original system.
Example 3. Let
![]() ( system with
potential and gyroscopic forces).
Solution
( system with
potential and gyroscopic forces).
Solution
![]() determines first integral
determines first integral
(i) equation
![]() are
are
![]() matrices )
always has symmetric nontrivial solution;
skewed-symmetric solution exists if matrix
matrices )
always has symmetric nontrivial solution;
skewed-symmetric solution exists if matrix ![]() has multiple eigenvalues
with corresponding prime elementary divisors and/or different Jordan blocks;
has multiple eigenvalues
with corresponding prime elementary divisors and/or different Jordan blocks;
(ii) equation
![]() has nontrivial solution
if some of roots of characteristic polynomial
has nontrivial solution
if some of roots of characteristic polynomial ![]() of matrix
of matrix
![]() are equal to zero and/or
are equal to zero and/or ![]() is even function.
is even function.
Let's discuss obvious variants for system (a) (14)-(16).
Variants 4.1.
![]() The solution of
The solution of ![]() would be
nontrivial if characteristic polynomial of matrix
would be
nontrivial if characteristic polynomial of matrix
![]() must be even or
must be even or
![]() ;
characteristic polynomial of matrix
;
characteristic polynomial of matrix
![]() must have multiple
roots ( if
must have multiple
roots ( if
![]() ).
Consequence of eqs. (14)-(16) is the equation:
).
Consequence of eqs. (14)-(16) is the equation:
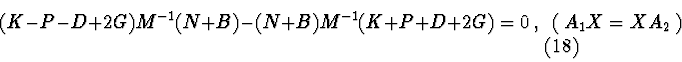
![]() are equal to zero;
are equal to zero;
![]() where
where ![]() are
eigenvalues of matrix
are
eigenvalues of matrix
![]() ,
,
![]() are eigenvalues of matrix
are eigenvalues of matrix
![]() The number of solutions is
The number of solutions is
![]() , where
, where
![]() is a power of
maximal common denominator
is a power of
maximal common denominator
![]() and
and
![]() of characteristic polynomials of these matrices. Let's build equations
of characteristic polynomials of these matrices. Let's build equations
![]() and find existence conditions for
and find existence conditions for ![]() equal to zero.
If the equation (18) has a solution
equal to zero.
If the equation (18) has a solution ![]() then also exist a
solution
then also exist a
solution
![]() , where matrix
, where matrix
![]() is commutative with
is commutative with ![]() ,
,
![]() is
commutative with
is
commutative with
![]()
Let's select symmetrical and skewed-symmetrical parts of solution
![]() and substitute them to equations (14) и (16). Then we
obtain conditions on system matrices.
and substitute them to equations (14) и (16). Then we
obtain conditions on system matrices.
Example 4.
4.1. Let
![]() (system with gyroscopic forces).
System (14)-(16) has solution
(system with gyroscopic forces).
System (14)-(16) has solution
![]() .
Equation (1) has first integral
.
Equation (1) has first integral
![]()
4.2. Let
![]() Then matrices
Then matrices
![]() are identical.
The task is reduced to calculation of matrices commutative with
are identical.
The task is reduced to calculation of matrices commutative with
![]() Also,
Also,
![]() Note that if
Note that if
![]() does not have multiple eigenvalues then
does not have multiple eigenvalues then
![]()
![]()
Variant 4.1.1. Let ![]() Then from eq. (14) follows
Then from eq. (14) follows
![]() This solution is possible if above-mentioned conditions are true:
characteristic polynomial of matrix
This solution is possible if above-mentioned conditions are true:
characteristic polynomial of matrix
![]() must be even or
must be even or
![]() ;
characteristic polynomial of matrix
;
characteristic polynomial of matrix
![]() must have multiple roots.
must have multiple roots.
Example 5.
5.1. Let
![]() ( system with gyroscopic
and potential forces ). System (14)-(16) has solution
( system with gyroscopic
and potential forces ). System (14)-(16) has solution
![]() That gives first integral of the equation (1)
That gives first integral of the equation (1)
![]()
5.2. Let
![]() Solution
Solution
![]() with
with
![]() determines first integral of equation
(1):
determines first integral of equation
(1):
![]()
![]()
Variant 4.2. Let ![]() . Then it remains a system of two
equations :
. Then it remains a system of two
equations :
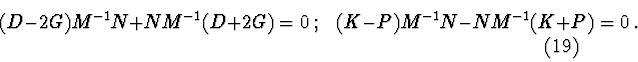
Example 6.
6.1. Let
![]() ( system with potential and gyroscopic
forces ).
Then in eq. (18)
( system with potential and gyroscopic
forces ).
Then in eq. (18)
![]() , characteristic polynomials of
matrices are identical.
There exist a solution
, characteristic polynomials of
matrices are identical.
There exist a solution
![]() that satisfies
eqs. (14) and (16). The system allows a first integral
that satisfies
eqs. (14) and (16). The system allows a first integral
![]() From theorems of Lyapunov's second method it follows that if
From theorems of Lyapunov's second method it follows that if ![]() then trivial solution of linear system (1) is stable with respect to
variables
then trivial solution of linear system (1) is stable with respect to
variables
![]() .
If matrix K is not definitely positive, we generate a bunch
of forms
.
If matrix K is not definitely positive, we generate a bunch
of forms ![]() and
and
![]() .
Conditions of sign-definitiveness of this band give sufficient
conditions of
stability for the critical system in question.
.
Conditions of sign-definitiveness of this band give sufficient
conditions of
stability for the critical system in question.
6.2. Let
![]() ( system with dissipative and gyroscopic forces).
System (19) has solution
( system with dissipative and gyroscopic forces).
System (19) has solution
![]() where
where
6.3. Let
![]() where
where
![]() (system with dissipative, gyroscopic and potential forces) and condition
(20) is met. Linear equation (1) has first integral
(system with dissipative, gyroscopic and potential forces) and condition
(20) is met. Linear equation (1) has first integral
Other variants of solutions of systems (a) and (b) are discussed in [2]. Integral of the linear system can be used as Lyapunov function for nonlinear system too.
The calculated first integrals (or their bunches) can be used to construct Lyapunov functions in proving the stability of the trivial solution for the system (1) if Sylvester's inequalities of sing-definiteness of the quadratic part of the integral (8) with respect to all variables of the problem are satisfied.
Systems with decomposition.
Let system (1) be separable to primary and secondary subsystems:
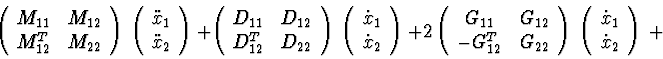
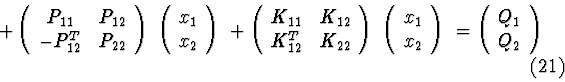
For example, if ![]() then from a differential consequence
then from a differential consequence
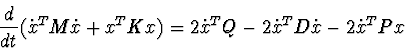
Theorem . If
![]() and set
and set
![]() does not contain full non-zero trajectory, then zero solution of a system
(21) (P=0) is asymptotically stable with respect to
does not contain full non-zero trajectory, then zero solution of a system
(21) (P=0) is asymptotically stable with respect to
![]() with any non-linear gyroscopic and potential forces.
with any non-linear gyroscopic and potential forces.
![]()
If ![]() then conditions of non-existence of full trajectory
on a set
then conditions of non-existence of full trajectory
on a set
![]() lead to the statement that a system
lead to the statement that a system
As it can be seen from presented theorems, studying of a system stability is reduced to searching of the conditions of sign-definitiveness, sign-constantness and equality to zero for matrices. Note that the task of sign-constantness for matrices cannot be solved on a computer without symbolic calculations. This is why existing numerical packages for stability investigation can work only with rough systems. This is also true for application of N.N. Krasovsky and other theorems based on Lyapunov functions with constant sign derivatives, where we must solve a question about absence of full trajectories of the system on some manifold.
Let's present one of possible algorithms for solution of this task.
1). Choosing a Lyapunov function
![]() and calculation
and calculation
![]() by equations of disturbed motion (1).
by equations of disturbed motion (1).
![]() Choosing a differential consequence .
Choosing a differential consequence .
2). Checking sign-constantness of a function
![]() ( if
( if
![]() then a group of values
then a group of values
![]() when
when
![]() will define a manifold we seek for).
will define a manifold we seek for).
3). If a manifold represents some surface
![]() then matrix condition:
then matrix condition:
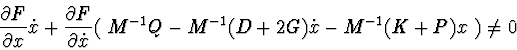
Note :
a). if during solution of specific tasks a sign-constant function
![]() can be factorized to
can be factorized to
![]() then instead of function
then instead of function ![]() (which determines a manifold equation)
we must use all independent situations
(which determines a manifold equation)
we must use all independent situations
![]() and investigate a question about non-existence of full trajectories for
each of them.
and investigate a question about non-existence of full trajectories for
each of them.
b). if ![]() isn't a function of all variables in the task, like
isn't a function of all variables in the task, like
![]() где
где
![]() then we can use
then we can use
![]()
![]() as the manifold for investigation.
as the manifold for investigation.
This algorithm is implemented in programming language of "Mathematica" system [6].
An example of using the "STABILITY" package.
We conduct parametric analysis of asymptotic stability
conditions of the equilibrium position of a satellite with controlled
gravitational stabilizer on circular orbit [7] (not considering elasticity of
the rod and without a gyrowheel in a satellite).
Linear equations of motion are subdivided to two subsystems.
In pitch angle (
![]() ) they have form
) they have form
If
![]() , then potential forces influence the system.
They are determined by forces of gravitational attraction and by the motion
along the orbit. Such a system cannot be asymptotically stable.
Indeed, the differential equations allow for the integral of energy
(example 6.1) :
, then potential forces influence the system.
They are determined by forces of gravitational attraction and by the motion
along the orbit. Such a system cannot be asymptotically stable.
Indeed, the differential equations allow for the integral of energy
(example 6.1) :
The requirements of definite positiveness of this quadratic form give conditions for secular stability of the system.
Let's consider following control actions at the attachment point:
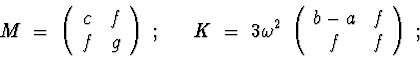
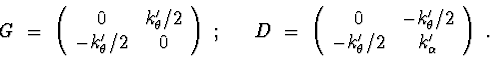
Let parameters of the system be :
![]() m ;
m ;
![]() m ;
m ;
![]()
![]() rad/s. ;
rad/s. ;
![]()
![]() With these values, domain where parameters
With these values, domain where parameters
![]() could be chosen is
presented on figure 1.
could be chosen is
presented on figure 1.
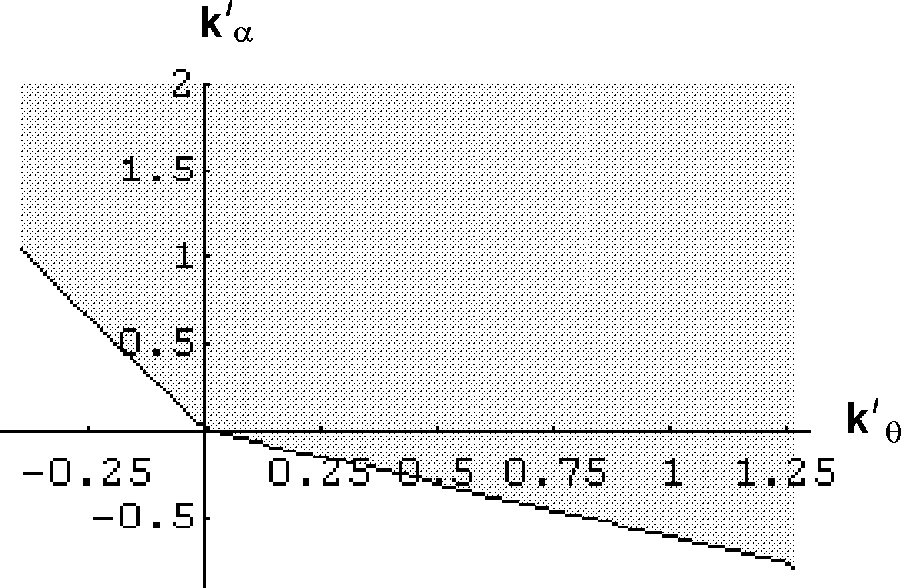
Figure 1.
This domain is found by program ![]() that plots 2D solutions of
numerical-symbolic algebraic inequalities (in this case Routh-Hurwitz
conditions).
that plots 2D solutions of
numerical-symbolic algebraic inequalities (in this case Routh-Hurwitz
conditions).
It is known that the problem about damping of transient process in the system
is connected with evaluation of the degree of stability (i.e. with the
evaluation of a disposition of the roots of characteristic equation
in left-hand half-plane).
Also there is an important task of choosing the parameters of the system
in question, so its degree of stability will be larger or equal than
a given value
![]() .
Let's study this question for the system (22).
For the characteristic equation
.
Let's study this question for the system (22).
For the characteristic equation
( where
![]() is the degree of stability (offset from
imaginary axis)) with the help of package "Stability" we obtained
Routh-Hurwitz conditions and made parametric analysis of these conditions.
The analysis showed, that the domain for choosing parameters
is the degree of stability (offset from
imaginary axis)) with the help of package "Stability" we obtained
Routh-Hurwitz conditions and made parametric analysis of these conditions.
The analysis showed, that the domain for choosing parameters
![]() exists only when
exists only when
![]() .
For example, when
.
For example, when
![]()
and the output of the program
will be the solution (domain) :
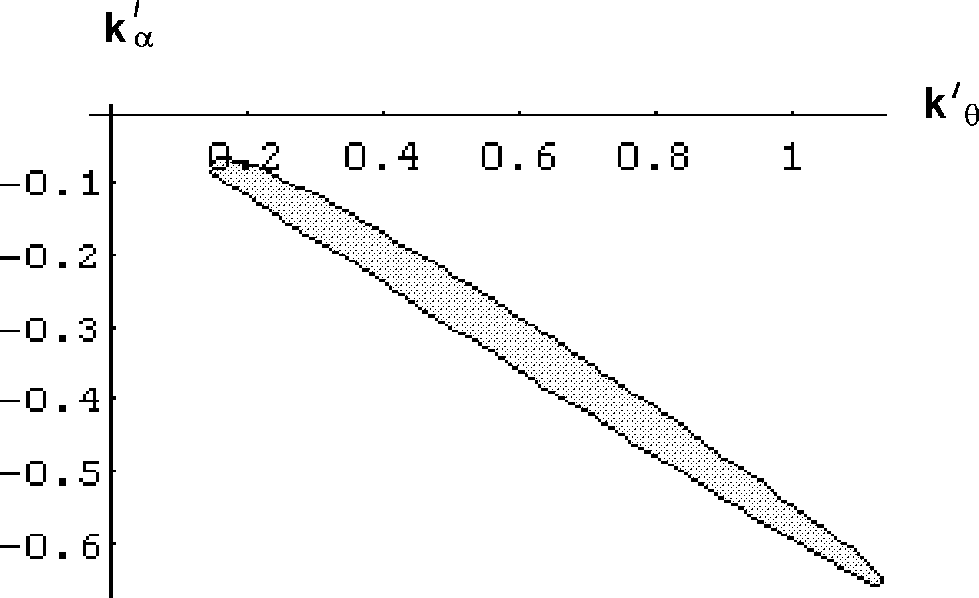
Figure 2.
On this picture it can be seen that asymptotical stability for given
degree of stability could be reached by adding an accelerating dissipative
force to the system, because
![]()
1. Banshchikov A.V., Bourlakova L.A. Information and Research System
"Stability". //Informations RAS. The theory and control systems. (Izvestia RAN.
Teoria i sistemi upravlenia.)
![]() (in Russian).
(in Russian).
2. Banshchikov A.V., Bourlakova L.A. On algorithms of symbolic computation
at the research of the stability. // Programming. (Programirovanie.)
![]() (in Russian).
(in Russian).
3. Meierov M.V. Criterion of an aperiodicity of regulation. // Izvestia AN SSSR.
Otdelenie tehnicheskix nauk. 1945.
![]() (in Russian).
(Bulletin DE L'ACADÉMIE DES SCIENSES DE L'URSS. Classe des sciences
techniques. )
(in Russian).
(Bulletin DE L'ACADÉMIE DES SCIENSES DE L'URSS. Classe des sciences
techniques. )
4. Lankaster P. Theory of matrices. Academic Press. New York - London, 1969.
5. Potapenko E.M. Robust stability of controlled dynamical systems.
// Izvestia RAN. Mehanika tverdogo tela.
![]() (in Russian).
(in Russian).
6. Wolfram S. Mathematica: A System for Doing Mathematics by Computer. Addison-Wesley Publ.Co. 1988.
7. Potapenko E.M. Dynamics of a spacecraft with line active control by a
gravitational stabilizer. // Space researches. (Kosmicheskie issledovania.)
![]() (in Russian).
(in Russian).