Let t be an independent variable and let y=y(t) be a dependent variable.
Let y(n) be the derivative of order n of y with respect to t. Let
Let
zi=exp(Qi) and let
vj=log(Rj), where
![]() and
and
![]() are polynomial functions with
coefficients in the same differential field F for all
are polynomial functions with
coefficients in the same differential field F for all
![]() and
all
and
all
![]() .
.
The ordinary differential equation
The equation ![]() is equivalent to the system
is equivalent to the system
Let
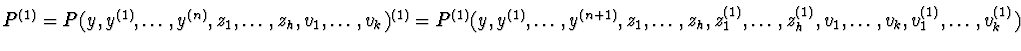 .
.
By algebraically eliminating
vk(1) between P(1) and
Rkvk(1)-Rk(1) and by using equalities
zi(1)=Qi(1)zi a polynomial
By algebraically eliminating vk between P and
P1' a polynomial
![]() is obtained.
is obtained.
By using this procedure we can
eliminate
![]() and we obtain a
polynomial Ph+k only in y and its derivatives, such that every
solution of
and we obtain a
polynomial Ph+k only in y and its derivatives, such that every
solution of ![]() is a solution of
is a solution of
![]() .
.
The same procedure can be applied to dynamical systems.
There are many differential elimination procedures. Some of them are based on
the characteristic set theory of Wu-Ritt [Ritt (1950,Kolchin (1973)]
[Wu (1987),Wu (1989),Wang (1993)];
other procedures use in addition the Gröbner bases theory for
polynomial ideals
[Boulier (1994),Boulier (1996)] [Boulier and Lazard and Ollivier and Petitot (1995),Diop (1991)]
[Diop (1991),Diop (1991),Diop (1992),Diop and Fliess (1991)]
[Fliess (1989),Fliess (1990)],
some others are based on the differential
resultants theory [Carra' Ferro (1997),Carra' Ferro (1997)] and the differential Gröbner bases
theory for differential polynomial ideals [Carra' Ferro (1987),Ollivier (1990),Weispfenning (1993)].