Evolving Algebras

Evolving Algebras have been proposed by Yuri Gurevich in 1988 [9,10] as models for arbitrary computational processes. They are finite, dynamic algebras representing state transitions and describing operational semantics of discrete dynamical systems. They may be tailored to any desired level of abstraction. System states are represented here as static algebras.

An evolving algebra is a structure

$$\psi=(\Sigma, S, I_0, T),$$

where:

• $\Sigma$ is a signature (a set of operational (or functional) symbols with their arities);
• S is a superuniverse, $\qquad \{true, false\} \subset S;$
• I₀ - an initial interpretation (a finite, static, many-sorted algebra);
• T - a set of transition rules.

I₀ gives an initial interpretation of the signature's operational symbols:

$$I_0: \Sigma \rightarrow \bigcup_{n \ge 0}(S^n \rightarrow S) \qquad \forall f \in \Sigma \quad I_0(f): S^n \rightarrow S.$$

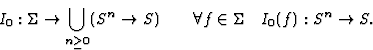
There are four kinds of transition rules (or updates):

1.

Function updates

$$f(t_1,\dots,t_n) := t_0 \qquad f \in \Sigma, \;\; n \ge 0$$

2.

Conditional

$$if \; b \; then \; C$$

3.

Extension of universes

$$extend \; U \subset S \; by \; x_1, \dots, x_m$$

4.

Contraction of universes

$$discard \; t \; from \; U$$

Iterative application of evolving algebra $\psi$ to sequentially arising states (static algebras) I_i, starting from the initial state I₀, may give a terminated computation:

$$I_0 \stackrel{\psi}{\longrightarrow} I_1 \stackrel{\psi}{\lo... ...\longrightarrow} \dots \stackrel{\psi}{\longrightarrow} I_M .$$

We plan to use the very flexible and powerful formalism of evolving algebras for description of our above-mentioned algorithms.