


Next: Iterated Function Systems as
Up: Automata Network Algorithm
Previous: Automata Network Algorithm
We define an Automata Network 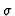 as a structure
as a structure
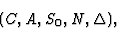 |
(11) |
where
- C is a set of cells;
- A is an alphabet of states (attributes);
-
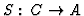 is a state,
is a state,  S0 - an initial state;
S0 - an initial state;
-
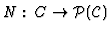 is a neighborhood system,
is a neighborhood system, 
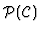 is the power-set of C,
is the power-set of C,
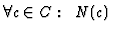 is the neighborhood of c;
is the neighborhood of c;
-
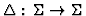 is a global dynamic
rule (GDR),
is a global dynamic
rule (GDR), 
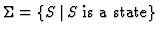 .
.
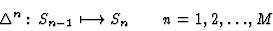 |
(12) |
The global dynamic rule 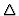 comes about from the local
dynamic rules (LDRs)
comes about from the local
dynamic rules (LDRs)
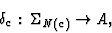 |
(13) |
where SN(c) is the restriction of S to N(c). Every LDR
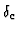 gives a new state value to the cell c as a function of
cell states from the neighborhood N(c) of c. The action of
gives a new state value to the cell c as a function of
cell states from the neighborhood N(c) of c. The action of
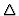
![\begin{displaymath}\Delta(S) = \bigcup_{c \in C}S[S(c) \leftarrow
\delta_c(S_{N(c)})],
\end{displaymath}](img70.gif) |
(14) |
is the union of the states obtained by replacing the state of each
cell c accordingly to 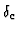 .
.
Automata Networks can be considered as a generalization of Cellular Automata,
the main difference is our automata networks have non-regular structure
of the system of the cell neighborhoods.
There is no a common template of vicinity for cells, the neighborhoods of
cells have variable cardinality and, hence, the LDRs have variable
arity. There are possible cases when
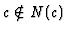 and even
and even
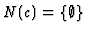 .
.
An automata network 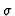 works as follows. If an initial state
S0 is given, it iteratively applies the GDR
works as follows. If an initial state
S0 is given, it iteratively applies the GDR 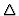 until it
reaches a steady attractive state SA:
until it
reaches a steady attractive state SA:
The cells work synchronously in parallel governed by some global
synchronization signals.



Next: Iterated Function Systems as
Up: Automata Network Algorithm
Previous: Automata Network Algorithm
IMACS ACA'98 Electronic Proceedings
![]() as a structure
as a structure
![]() comes about from the local
dynamic rules (LDRs)
comes about from the local
dynamic rules (LDRs)
![]() and even
and even
![]() .
.
![]() works as follows. If an initial state
S0 is given, it iteratively applies the GDR
works as follows. If an initial state
S0 is given, it iteratively applies the GDR ![]() until it
reaches a steady attractive state SA:
until it
reaches a steady attractive state SA: