Introduction.

Many practical problems can be easily solved if we are able to find the solution of an algebraic system of equations with parametric coefficients for any (or for many) values of the parameters. In these problems the use of Gröbner Bases techniques to rewrite the given equations in easier ways (for example, in triangular form) have to be completed with other techniques to determine which are the values of the parameters that preserve the good properties of the Gröbner bases computations. In this paper we address this question, for the case of homogeneous polynomial systems, by focusing our attention to the using of the already available tools inside the FRISCO framework [5] such as the PoSSoLib. As a final result it is obtained an efficient implementation dealing with the problem of solving a homogeneous polynomial system of equations containing parameters when using Gröbner Bases as the main tool. Let 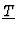$\underline{T}$ be the parameters $(T_1,\ldots,T_s)$ and $\underline{X}=(X_1,\ldots,X_n)$ the unknowns. The problem to solve is the determination (whatever it means and to be clarified later) of the solution set of the polynomial system of equations:

$$\matrix{F_1(\underline{T},X_1,\ldots,X_n)&\!\!\!\!=0\cr F_2... ...l\vdots\;\cr F_m(\underline{T},X_1,\ldots,X_n)&\!\!\!\!=0\cr}$$

where the F_i's are homogeneous polynomials in the variables 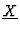$\underline{X}$. Two different questions arise naturally in this context: first, to get the conditions the parameters must verify in order the considered homogeneous system has a solution and, second, to describe, in some way, the solutions, i.e., the dependency between every unknown and the parameters. Different methods can be found in the Computer Algebra literature addressing this problem in general (not only for the homogeneous case). Mainly:

• To use Comprehensive Gröbner Bases (see [14]).
  • The notion of Comprehensive Gröbner Bases (see [14]) is exactly, if it is easy to compute, what we want to obtain: an explicit partition of the parameter space together with a Gröbner Basis of the considered ideal, already specialized, for every subset in such partition. The main problem with this approach is that, in its general version, is highly inefficient due mainly to the big number of sets appearing in such partition.
• To use the Dynamic Evaluation Method (see [4]).
  • By using only ``well parametrized" gcd computations and a ``case by case" methodology, a complete description of the solution set is obtained in terms of conditions on the parameters.
• To use multivariate resultants (see [13]).
  • The usual techniques based upon resultants work only when the numbers of equations and unknowns are equal, they require the computation of determinants of matrices with a very big size and polynomial entries and, initially, they only provide the conditions on the parameter space in order the considered system has a solution.
• To use triangular sets (see [8]and the references contained there) .
  • It is close in spirit to the Dynamic Evaluation Method before mentioned but stronger algebraic techniques are used in order to remove multiplicities from the different solution sets which helps to improve the efficiency of the method.
• To use specific Linear Algebra tools for parametric linear systems (see [11]).
  • An ad-hoc using of Cramer's rule together with a parameter dependent rank computation of matrices with polynomial entries provide a specific solution for this case.

In this paper our goal is to show how, with a not very expensive cost, the using of Gröbner Bases can help to get answers when trying to describe the solution set of the considered homogeneous system in terms of the parameters. Since the tool chosen to be used is the computation of Gröbner Bases, the first section presents, in an unified way, the behaviour of Gröbner Bases under specialization. Two strategies can be initially adopted:

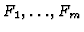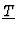• To compute a Gröbner Basis of the ideal generated by the polynomials $F_1,\ldots,F_m$ in ${\mathchoice {\setbox 0=\hbox{$\displaystyle\rm Q$ }\hbox {\raise 0.15\ht0\hbo... ...pt{\kern0.4\wd0\vrule height0.7\ht0\hss}\box0}}}(\underline{T})[X_1,\ldots,X_n]$ (with respect to any monomial ordering) together with the ``good" specialization conditions on $\underline{T}$ (see [3]).
• To compute a Gröbner Basis of the ideal generated by the polynomials 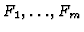$F_1,\ldots,F_m$ in ${\mathchoice {\setbox 0=\hbox{$\displaystyle\rm Q$ }\hbox {\raise 0.15\ht0\hbo... ...0pt{\kern0.4\wd0\vrule height0.7\ht0\hss}\box0}}}[\underline{T},X_1,\ldots,X_n]$ (with respect to any monomial ordering) together with the ``good" specialization conditions on 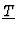$\underline{T}$. Anyway, the new system is always equivalent to the first one, even if it is not a Gröbner Basis (see [7] or [9]).

and their analysis is done is the first section. This section shows also how to adapt the strategy in [6] to avoid the growing the coefficients in the Gröbner Basis in order to get a list of open conditions on the parameter space where a Gröbner Basis is available after specialization. The second section contains the main result of this paper: it is shown, when working in ${\mathchoice {\setbox 0=\hbox{$\displaystyle\rm Q$ }\hbox {\raise 0.15\ht0\hbo... ...0pt{\kern0.4\wd0\vrule height0.7\ht0\hss}\box0}}}[\underline{T},X_1,\ldots,X_n]$, how to use the Hilbert Function in order to obtain a set of conditions on the parameters providing that the specialization of a ``generic" Gröbner Basis in such polynomial ring is again a Gröbner Basis of the specialized homogeneous polynomial system. Last two sections are devoted, first, to indicate to use these techniques to deal with polynomial system solving involving parameters and homogeneous polynomials and, second, to present the implementation of these algorithms in the PoSSoLib.