The best result, when working in
![${\rm I\kern -2.2pt K\hskip 1pt}(\underline{T})[\underline{X}]$](img34.gif) ,
that
we have found appears in [3] (pp. 277, Exercises 5 to 9),
where it is proposed an algorithmic method to compute a subset
,
that
we have found appears in [3] (pp. 277, Exercises 5 to 9),
where it is proposed an algorithmic method to compute a subset
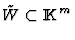 such that if
such that if
![$\tilde
G=\{\tilde g_1(\underline{X}),\dots,\tilde
g_s(\underline{X})\}\subset{\rm I\kern -2.2pt K\hskip 1pt}(\underline{T})[\underline{X}]$](img36.gif) is a Gröbner
basis of the ideal
is a Gröbner
basis of the ideal
![$\tilde I=<\tilde F_1(\underline{X}),\dots,\tilde
F_m(\underline{X})>\subset{\rm I\kern -2.2pt K\hskip 1pt}(\underline{T})[\underline{X}]$](img37.gif) ,
and
,
and
 ,
then
,
then
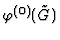 is a Gröbner basis of
is a Gröbner basis of
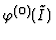 .
This set
.
This set
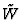 of sufficient conditions on the parameters is defined by:
of sufficient conditions on the parameters is defined by:
- a)
- none of the denominators of
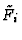 are 0,
are 0,
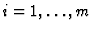 ,
,
- b)
- none of the denominators of
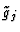 are 0,
are 0,
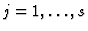 ,
,
- c)
- let Bij be the polynomials in
![${\rm I\kern -2.2pt K\hskip 1pt}(\underline{T})[\underline{X}]$](img34.gif) such that
such that
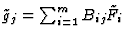 ;
none of the denominators of Bij are 0.
;
none of the denominators of Bij are 0.
Although the computation of the denominators appearing in the
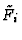 's and the
's and the
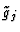 's is easy, the computation of the denominators
in the Bij's can lead to lengthy calculations: we have to compute one
quotient ideal (
's is easy, the computation of the denominators
in the Bij's can lead to lengthy calculations: we have to compute one
quotient ideal (
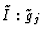 )
and one elimination ideal (
)
and one elimination ideal (
![$\tilde
I:\tilde g_j\cap {\rm I\kern -2.2pt K\hskip 1pt}[\underline{T}]$](img48.gif) )
for every polynomial
)
for every polynomial
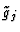 in
the basis.
in
the basis.
IMACS ACA'98 Electronic Proceedings