M. Kalkbrener (see [9]) proposes a slightly
different approach, as he considers that the specialization map has the
following domain and image:
where R is a
Noetherian commutative ring (
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T}]$](img72.gif) in our case) and
in our case) and
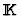 is
a field, and
a Gröbner basis G of I in
is
a field, and
a Gröbner basis G of I in
![$R[\underline{X}]$](img73.gif) with respect to any
ordering in the monomials of
with respect to any
ordering in the monomials of
![$R[\underline{X}]$](img73.gif) (note that in this case Kalkbrener's approach requires the
computation of a Gröbner Basis in
(note that in this case Kalkbrener's approach requires the
computation of a Gröbner Basis in
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T}][\underline{X}]$](img74.gif) ). The
question to answer is: when is
). The
question to answer is: when is
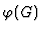 a Gröbner basis of
a Gröbner basis of
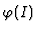 ?, and the answer is
similar to Gianni's one: in [9] it is shown that
this is is equivalent to the following:
?, and the answer is
similar to Gianni's one: in [9] it is shown that
this is is equivalent to the following:
assume that the gi's are ordered in such a way that there
exists one
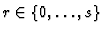 with
with
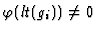 for
for
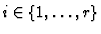 , and
, and
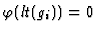 for
for
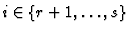 . Then, for every
. Then, for every
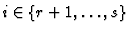 the polynomial
the polynomial
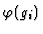 is reducible to 0 modulo
is reducible to 0 modulo
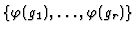 .
.
But remark that in order to test this condition, we need to compute a
Gröbner basis of
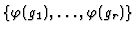 ,
but this can be,
in the worst case, similar to compute a Gröbner basis of
,
but this can be,
in the worst case, similar to compute a Gröbner basis of
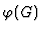 ,
unless in the case in which r=s, where we can directly conclude that
,
unless in the case in which r=s, where we can directly conclude that
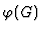 is a Gröbner basis.
Although this approach seems to contain in particular Gianni's one, remark
that G is a Gröbner basis in
is a Gröbner basis.
Although this approach seems to contain in particular Gianni's one, remark
that G is a Gröbner basis in
![$R[\underline{X}]$](img73.gif) with
with
![$R={\rm I\kern -2.2pt K\hskip 1pt}[\underline{T}]$](img82.gif) ,
which implies
that it requires the computation of a Gröbner Basis over an integral
domain (
,
which implies
that it requires the computation of a Gröbner Basis over an integral
domain (
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T}]$](img72.gif) )
and not over a field which is the usual case: in
[1] or in [2] it is described how to compute such Gröbner Bases.
)
and not over a field which is the usual case: in
[1] or in [2] it is described how to compute such Gröbner Bases.
IMACS ACA'98 Electronic Proceedings
with
for
, and
for
. Then, for every
the polynomial
is reducible to 0 modulo
.