Computation of Moduli, Periods and Modular Symbols

Nikolaj M. Glazunov

Glushkov Institute of Cybernetics NAS
252650 Ukraine Kiev GSP-650 Glushkov prospekt 40
Email: glanm@d105.icyb.kiev.ua

Abstract

The subject matter of this communication lies in the area of computation moduli, periods and modular symbols of algebraic curves. Let S be the Riemann surface of algebraic curve C of genus g. The set of 6g - 6 real parameters which determines the conformal class of the surface S is called the moduli of C. For instance, the moduli of elliptic curve over complex numbers is its modular invariant. The integral of integer holomorphic differential of C along generator of 1-homology group of S is the period of C. Periods of C determine the Jacobian variety of C. The set of all periods of curves of given genus determines the space of periods. There is a mapping from moduli variety of curves of given genus to their space of periods (morphism of periods). By Torelli theorem the morphism is an inclusion.
An integral of holomorphic differential 1-form along geodesic line connecting angles of a compact Riemann surface is a modular symbol. The modular symbols was introduced by B. Birch. Modular symbols for computation of periods of modular forms of weight 2 were considered and investigate by Ju. Manin, H. Swinnerton-Dyer and B. Mazur. Some Manin's results were generalized by V. Drinfel'd and V. Shokurov.
The A. Wiles proving of Shimura-Taniyama conjecture gives possibility of computation of the number of generators of Mordell-Weil group of elliptic curves over 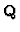$\bf Q$. By D. Goldfeld the modular symbols can be computed in polynomial time.
On the base of investigation of the results the problems of computation of modular symbols are discussed. Algorithms have been developed for computation of (i) moduli and periods of elliptic curves and algebraic curves of genus 2 and 3; (ii) modular symbols of modular forms of the weight grater or equal 2. Computation of moduli, periods and modular symbols are included.