Simulating Membranes with MPM

Fluid-Membrane systems are common and include parachutes, vehicle airbags, high-speed magnetic tapes, printing presses, inflatable structures, blood vessels and bladder tanks. These systems are especially difficult to model numerically when the membrane deforms substantially and has an effect on the fluid flow.

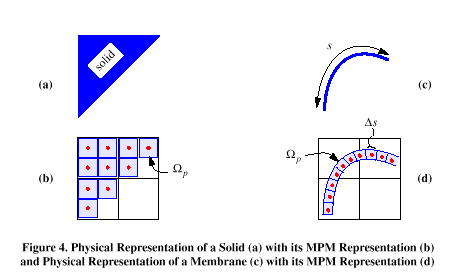
In the Material-Point Method (MPM), a mesh of Lagrangian material points is used to discretize solid bodies, membranes or fluid. In the figure below, the red material points represent a discretization of the solid, blue body.

The interaction between these points is solved by interpolating information from the points to a background mesh where equations of motion are solved. Information from the mesh solution updates the material points. Material points carry mass, velocity, strain and stress. The stress results in internal forces at mesh nodes. The momentum equation is solved on the mesh by taking into account internal forces from all nearby materials.

On boundaries between fluid and the structure, the internal forces in mixed solid-fluid elements determine the interface conditions. Material points within the same computational element at a given timestep will see the same increment in strain, but can have different stress because each material point follows its own constitutive equation. The constitutive equation for a membrane point is similar to that for a solid, except the strain increment is projected onto the local, normal-tangential coordinate system for the membrane and only the tangential components of the strain contribute to the stress.