


Next: An Example of HRFA
Up: Accuracy Analysis of Hybrid
Previous: Approximate-GCD by Hribernig and
By definition 3.1 and the algorithm 3.1,
the hybrid rational function, p(x)/q(x), with the accuracy level
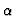 is obtained. We consider, here, the error between p(x)/q(x)and the interpolated rational function, P(x)/Q(x). The following
theorem is established.
is obtained. We consider, here, the error between p(x)/q(x)and the interpolated rational function, P(x)/Q(x). The following
theorem is established.
Theorem 4.1
Let
P(
x) and
Q(
x) be polynomials in
C[
x] and let
p(
x) and
q(
x) be polynomials
satisfying
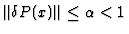
and
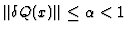
in (
8). Then
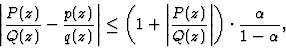 |
(9) |
for
![$z\in[-1,1]$](img53.gif)
s.t.
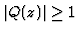
.
proof
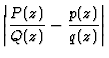 |
= |
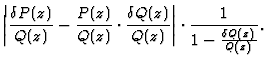 |
(10) |
The relaxed termination
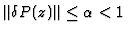 and
and
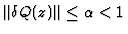 implies
implies
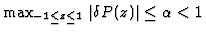 and
and
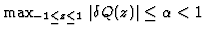 respectively.
Thus, rhs of (10) is estimated by (9),
for
respectively.
Thus, rhs of (10) is estimated by (9),
for
![$z\in[-1,1]$](img53.gif) s.t.
s.t.
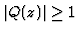 .
.

This theorem 4.1 gives the error of HRFA and is the main
result of this paper. To show how apparent the error is,
we rewrite HRFA algorithm, Algorithm 2.1,
as follows:
Algorithm 4.1 (HRFA by near-GCD)
Input: data set
D s.t.
![$x_i\in [-1,1]$](img62.gif)
and parameter
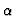 Output:
Output: numerical rational interpolation
p(
x)/
q(
x)
Method:
- 1.
- Compute rational interpolation P(x)/Q(x) to interpolate D.
- 2.
- Let
f1=P(x),f2=Q(x) input polynomials of algorithm 3.1. Compute
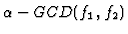 and obtain
and obtain
p(x)/q(x)=s(1)j/s(2)j.
After the computation of the procedure 1. of
the algorithm 4.1,
accuracy of numerical rational interpolation p(x)/q(x) of the data set
D is estimated by Theorem 4.1 as
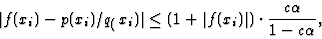 |
(11) |
where positive constant c satisfies the condition
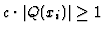 for
for
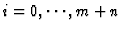 .
.
The result (11) shows that our a posteriori error estimate
is dominated by the parameter, the accuracy level, 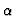 .
Similar results may obtained by using other approximate-GCDs
but with different accuracy level parameters.
.
Similar results may obtained by using other approximate-GCDs
but with different accuracy level parameters.



Next: An Example of HRFA
Up: Accuracy Analysis of Hybrid
Previous: Approximate-GCD by Hribernig and
IMACS ACA'98 Electronic Proceedings
![]() is obtained. We consider, here, the error between p(x)/q(x)and the interpolated rational function, P(x)/Q(x). The following
theorem is established.
is obtained. We consider, here, the error between p(x)/q(x)and the interpolated rational function, P(x)/Q(x). The following
theorem is established.
![]() .
Similar results may obtained by using other approximate-GCDs
but with different accuracy level parameters.
.
Similar results may obtained by using other approximate-GCDs
but with different accuracy level parameters.