First, we present a general approach to the design of stabilizing switched controllers for systems (1) which are based on the basic controllers (2). It turns out that if we always can choose a basic controller such that a positive definite function decreases along trajectories then the system can be stabilized by switching basic controllers.
To be able to formulate the problem of stabilizing a system by
switching basic controllers in a way suitable for quantifier
elimination, we will use the following theorem. In the sequel we let
denote the gradient of V w.r.t. x.
ProofIntroduce the sets
Since 
is continuous, these sets are open. Let
and consider 
. According to the assumptions, any 
belongs to some 
.
Since is open, there is an 
and
such that 
. The collection
forms an open cover of . Since is compact, there exists a finite subcover
. The collection
is also a cover. Now,
in each 
we have 
for at least one of the functions, which also attains
its maximum in this set. Hence
where 
. We conclude that for any there
exists such that for any 
there is an such
that
Let 
denote a solution starting at 
at time 0 of the
system (1) controlled by switching basic controllers such
that (7) is satisfied. Furthermore, let 
denote the time derivative of V(x) along a solution.
According to (8) we have 
for all points on the trajectory in . Integrating this inequality from 0
to t gives
This shows that can only stay in for a finite time, since V is bounded from
below. Since 
is invariant (V is decreasing along
solutions) the trajectory has to enter 
. Hence,
since was
arbitrary, i.e., the origin is attractive.
To prove stability we observe that 
is invariant. Moreover, there exists 
and
such that 
, since V is
positive definite, see for example [8].
We conclude that the origin is an asymptotically stable solution and
is a region of attraction of the system (1).
The assumptions in the theorem implies that the domains of definition
of the control laws cover , i.e., 
.
Notice that each of the basic controllers may yield an unstable closed loop system but there may still exist a switched stabilizing strategy. The following corollary follows easily from the proof of Theorem 1 since all sublevel sets of a function, which is radially unbounded, are compact.
If the assumptions in Theorem 1 or Corollary 1 are satisfied then the following controller can be used to stabilize the system
With this choice we get 
for
all 
. Observe that the switching
function I might be multiple valued since the minimum
in (10) might be obtained by several controllers
simultaneously. This is the case along switching surfaces. For states
corresponding to multiple values the behavior of the controller has to
be further specified. Either techniques from sliding mode
control [16] can be used or a slight variation of
controller (10) where hysteresis is introduced. Due
to the fact that the sets (introduced in the proof of
Theorem 1) are open, the switching surfaces of
controller (10) can be substituted by hysteresis
zones. This will prevent sliding modes but chattering solutions may
appear instead depending on the direction of the vector fields along
the switching surface, see Example 3.
The conditions in Theorem 1 and Corollary 1 can be checked by quantifier elimination if the functions that appear in the theorems can be described by semialgebraic sets. This means that we are able to handle feedback control laws which are implicitly defined as solutions to multivariate polynomial equations. In connection to stabilization of the zero dynamics of a nonlinear system, which is not affine in the control, this turns out to be very useful, see Section 4.
The decision problem that has to be solved to verify the conditions of Theorem 1 is
and for Corollary 1 we get
If 
is an algebraic function of x, i.e., if the relation between
and x is a polynomial equation 
and is one
of the roots, the above formulas have to be modified. We have to
quantify u and 
is changed to 
, see Example 4.
Furthermore, given a family of parameterized positive definite
functions 
we can use quantifier elimination to
determine if there exists a function in this family such that it
satisfies the conditions in Theorem 1 or
Corollary 1. For instance, in order to check global
stabilizability using the family of quadratic positive definite
functions, 
, we consider the following decision
problem
where P is a matrix variable and 
denotes a set of inequalities which guarantee that P is positive
definite, e.g., the positiveness of the principal diagonal minors of P.
This procedure is much more general than when we just use one fixed function V(x). The main drawback of this approach is the large number of variables in the formula. The number of variables is equal to the sum of the number of states, n, and the number of parameters we need to describe V(x). In the quadratic case we get n+n(n+1)/2-1 variables.
To reduce the required computations, we can search for a quadratic Lyapunov function for the linearized switched dynamics and then use this in the decision problem (11). The following results from [11, 14] are then useful.
ProofSee [11].
The results above and in particular the linearization result of
Lemma 2 can be used to considerably reduce the
required computations of the stabilizability test. Indeed, in order to
test stabilizability it is easier if one uses linearizations but the
design of a stabilizing controller and the estimation of the domain of
attraction can be done directly by using quantifier elimination. We
propose the following procedure:
are denoted
. Check
whether the following decision problem is TRUE
Note that the problem can be normalized by fixing one of the
to 1, which reduces the number of variables.
can be extracted from the
quantifier elimination procedure. Take any such solution .
Since the matrix 
is Hurwitz, it satisfies the
Lyapunov matrix equation. Given any symmetric and positive definite
matrix 
, there exists a unique solution P to
which is symmetric and positive definite. Fix the matrix Q and compute P.
Performing quantifier elimination gives an estimate of the domain of attraction, since the resulting constraints on r correspond to invariant ellipsoids such that all trajectories starting in such an ellipsoid converge to the origin.
and the matrix Q in the above procedure are
design parameters which can be chosen differently in order to obtain
other estimates of the domain of attraction. The method proposed above
cannot be used if the linearization matrices 
do not satisfy the
conditions of Lemma 2.
Consider the two nonlinear systems 
where
The linearization matrices are
which both are unstable. However, 
is Hurwitz and we can
switch between the two systems to stabilize the system locally
according to Lemma 2. It is easy to see that
P=I solves the Lyapunov equation (19). To estimate
the domain of attraction we utilize formula (20)
and get 0 < r < 1.0552. Hence, within a circle of radius at least
1.055 we can control the state to the origin.
Lemma 2 may only be used in situations when the linearizations of the continuous dynamics contain enough structure. However, these conditions are not satisfied in general and quantifier elimination is the only tool, which we are aware of, that can handle these cases.
Lemma 2 cannot be used for the system where
since the linearizations do not contain enough information about the
system behavior near the origin. We have to use
Theorem 1 or Corollary 1 directly
instead. We try with the Lyapunov candidate function
. Performing quantifier elimination in
formula (12) gives TRUE, which shows that the
system is globally stabilizable by switching basic controllers.
In Figure 1 we illustrate the regions where 
and 
. The union of the gray-shaded regions
covers the whole state space.
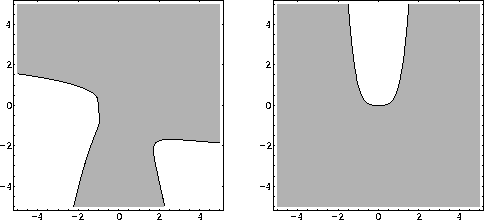
Figure 2: The regions (gray) where (left) and
(right).
The curve 
can be shown to lie in the interior of
the overlap of the regions in Figure 1 and can
hence be used to switch between the systems to obtain global
asymptotical stability.
