


Next: Nonalgebraic Ordinary Differential Equations
Up: Systems of Nonlinear and
Previous: Introduction
We assume that everything, which is undefined, is as in [Ritt (1950] and
in [Kolchin (1973)].
Let 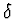 be a derivation operator and let R be a differential
ring, i.e. a commutative ring with unit and a derivation
be a derivation operator and let R be a differential
ring, i.e. a commutative ring with unit and a derivation 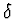 acting
on it, such that the field of rational numbers
acting
on it, such that the field of rational numbers 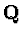 is contained in R.
is contained in R.
A differential field F is a field, which is also a differential ring.
Let CR={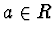 :
:
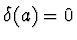 } be the
ring of constants of R and let
} be the
ring of constants of R and let
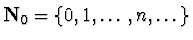 .
.
REMARK 1
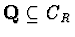
because
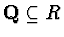
.
EXAMPLE 1
R=
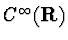
,
R=
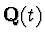
,
R=
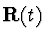
and
R=field of the meromorphic functions on a domain of
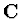
with
the usual derivation
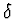
=
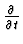
are
differential rings.
R=
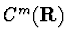
for all
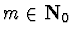
is not a differential ring.
If
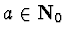 ,
then order of
,
then order of
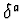 is ord(
is ord(
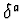 )=a.
)=a.
DEFINITION 1
S=
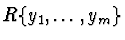
=
R[
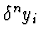
:
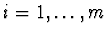
and
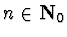
]
is the
differential ring of the differential polynomials in the differential
indeterminates
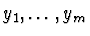
with coefficients in the
differential ring
R.
If 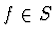 ,
then order of f is ord(f)=max{
,
then order of f is ord(f)=max{
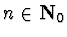 :
f contains a power product in
:
f contains a power product in
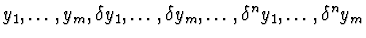 with
nonzero coefficient }.
with
nonzero coefficient }.
DEFINITION 2
An ideal
I of
S is a differential ideal iff
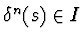
for all
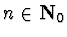
and all
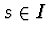
.
If
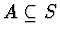
,
then [
A]=(
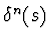
:
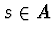
,
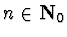
) denotes the smallest
differential ideal containing
A.
Let R be a differential ring of functions in the independent variable t,
let 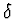 =
=
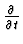 and let y=y(t) be a differential
indeterminate. y(n)=
and let y=y(t) be a differential
indeterminate. y(n)=
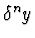 is the derivative of order n of ywith respect to t for all positive integers n, while
y(0)=
is the derivative of order n of ywith respect to t for all positive integers n, while
y(0)=
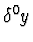 =y.
=y.
So an ordinary algebraic differential equation in m dependent variables
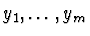 with coefficients in R is nothing else than
the equality
with coefficients in R is nothing else than
the equality 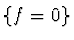 for some differential polynomial f in S.
for some differential polynomial f in S.



Next: Nonalgebraic Ordinary Differential Equations
Up: Systems of Nonlinear and
Previous: Introduction
IMACS ACA'98 Electronic Proceedings
![]() :
:
![]() } be the
ring of constants of R and let
} be the
ring of constants of R and let
![]() .
.
![]() ,
then order of
,
then order of
![]() is ord(
is ord(
![]() )=a.
)=a.
![]() ,
then order of f is ord(f)=max{
,
then order of f is ord(f)=max{
![]() :
f contains a power product in
:
f contains a power product in
![]() with
nonzero coefficient }.
with
nonzero coefficient }.
![]() =
=
![]() and let y=y(t) be a differential
indeterminate. y(n)=
and let y=y(t) be a differential
indeterminate. y(n)=
![]() is the derivative of order n of ywith respect to t for all positive integers n, while
y(0)=
is the derivative of order n of ywith respect to t for all positive integers n, while
y(0)=
![]() =y.
=y.
![]() with coefficients in R is nothing else than
the equality
with coefficients in R is nothing else than
the equality ![]() for some differential polynomial f in S.
for some differential polynomial f in S.