


Next: Numeric part
Up: Symbolic part
Previous: Reduction tree
Design variables whose values should be changed
From the viewpoint of supporting design, detecting inconsistent inequalities is not sufficient help to a designer. Especically in embodiment design, it is quite important for a designer to know what variable values are not appropriate. This section describes the method of finding out design variables whose values should be changed.
Suppose that
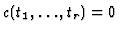 is an equation showing inconsistency among inequalities. Assignment of a concrete value to a design variable is expressed as a univariate linear equation. That is, univariate linear equation ``xk=a'' means ``a is assigned to xk''. Thus, by searching for univariate linear equations used for computing
is an equation showing inconsistency among inequalities. Assignment of a concrete value to a design variable is expressed as a univariate linear equation. That is, univariate linear equation ``xk=a'' means ``a is assigned to xk''. Thus, by searching for univariate linear equations used for computing
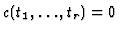 ,
design variables whose values should be changed can be found out. If ``xk=a'' is used to obtain
,
design variables whose values should be changed can be found out. If ``xk=a'' is used to obtain
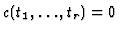 ,
``xk=a'' has something to do with the inconsistency. Otherwise, ``xk=a'' has nothing to do with it.
,
``xk=a'' has something to do with the inconsistency. Otherwise, ``xk=a'' has nothing to do with it.
Let C be the whole constraint set including univariate linear equations. Obviously,
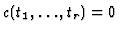 belongs to the ideal defined by C. If
belongs to the ideal defined by C. If
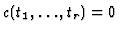 does not belong to the ideal defined by
does not belong to the ideal defined by
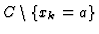 ,
it is concluded that xk=a is used to compute
,
it is concluded that xk=a is used to compute
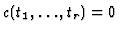 .
Otherwise, xk=a is not necessary to obtain
.
Otherwise, xk=a is not necessary to obtain
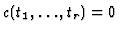 .
Therefore, design variables whose values should be changed are found out according to the following procedures.
.
Therefore, design variables whose values should be changed are found out according to the following procedures.
Method of detecting design variables whose values should be changed
- 1.
- Let C be the whole constraint set Eq. (2), and U be a set of univariate linear equations included in C. Suppose that
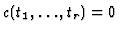 is the equation which shows inconsistency among inequalities in Eq. (1). Let E be an empty set.
is the equation which shows inconsistency among inequalities in Eq. (1). Let E be an empty set.
- 2.
- If U is empty, return E.
- 3.
- Let xk=a be the first element in U, and U be
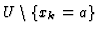 .
.
- 4.
- The Gröbner base G of
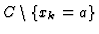 is computed.
is computed.
- 5.
- Let
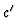 be a normal form of
be a normal form of
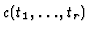 by G. If
by G. If
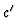 is not 0, let E be
is not 0, let E be
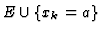 .
.
- 6.
- Go back to Step 2.




Next: Numeric part
Up: Symbolic part
Previous: Reduction tree
IMACS ACA'98 Electronic Proceedings
![]() is an equation showing inconsistency among inequalities. Assignment of a concrete value to a design variable is expressed as a univariate linear equation. That is, univariate linear equation ``xk=a'' means ``a is assigned to xk''. Thus, by searching for univariate linear equations used for computing
is an equation showing inconsistency among inequalities. Assignment of a concrete value to a design variable is expressed as a univariate linear equation. That is, univariate linear equation ``xk=a'' means ``a is assigned to xk''. Thus, by searching for univariate linear equations used for computing
![]() ,
design variables whose values should be changed can be found out. If ``xk=a'' is used to obtain
,
design variables whose values should be changed can be found out. If ``xk=a'' is used to obtain
![]() ,
``xk=a'' has something to do with the inconsistency. Otherwise, ``xk=a'' has nothing to do with it.
,
``xk=a'' has something to do with the inconsistency. Otherwise, ``xk=a'' has nothing to do with it.
![]() belongs to the ideal defined by C. If
belongs to the ideal defined by C. If
![]() does not belong to the ideal defined by
does not belong to the ideal defined by
![]() ,
it is concluded that xk=a is used to compute
,
it is concluded that xk=a is used to compute
![]() .
Otherwise, xk=a is not necessary to obtain
.
Otherwise, xk=a is not necessary to obtain
![]() .
Therefore, design variables whose values should be changed are found out according to the following procedures.
.
Therefore, design variables whose values should be changed are found out according to the following procedures.