


Next: Accuracy of HRFA
Up: Accuracy Analysis of Hybrid
Previous: Hybrid Rational Function Approximation
The approximate-GCD, which is called near-GCD in [8],
of two polynomials
![$f_1, f_2 \in C[x]$](img29.gif) ,
where C[x] is a complex number coefficient polynomial,
is stated as the following concept.
,
where C[x] is a complex number coefficient polynomial,
is stated as the following concept.
Definition 3.1 (Hribernig and Stetter)
At the accuracy level
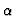
,
two polynomials
![$\tilde{f}_i\in C[x]$](img31.gif)
,
i=1,2, possess a near-GCD

if there exist polynomials
![$f^{\ast}_i\in C[x]$](img33.gif)
,
i=1,2, which satisfy
 |
(5) |
and deg

is the highest possible degree for (
5).
Equivalently, a near-GCD

of

and

satisfies
 |
(6) |
A near-GCD at accuracy level
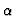
will be denoted by

.
Here, the norm of the polynomial means L1 norm. A near-GCD  is
computed via
Euclidean Algorithm and a relaxed
termination criterion which should be imposed at a given accuracy level
is
computed via
Euclidean Algorithm and a relaxed
termination criterion which should be imposed at a given accuracy level 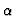 .
The
algorithm to compute
.
The
algorithm to compute 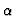 -GCD of f1 and f2 is summarized as follows:
-GCD of f1 and f2 is summarized as follows:
Algorithm 3.1 (tex2html_wrap_inline$$-GCD)
Input:
 Output:
Output: 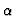
-GCD of
f1 and
f2
Method:
- 1.
- Compute
and
for
 and i=1,2 with
and i=1,2 with
si-1(i)=0, si(i)=1.
- 2.
- if
 ,
then
,
then
The polynomials fj generated by the algorithm,
f1 and f2 are represented as
 |
(7) |
In our case, f1 and f2 should be read as P(x) and Q(x), respectively.
Also s(1)j,s(2)j, and fj should be read as p(x), q(x) and g(x), respectively.
Therefore (7) is expressed as
 |
(8) |
where
 and
and
 .
.



Next: Accuracy of HRFA
Up: Accuracy Analysis of Hybrid
Previous: Hybrid Rational Function Approximation
IMACS ACA'98 Electronic Proceedings
![]() ,
where C[x] is a complex number coefficient polynomial,
is stated as the following concept.
,
where C[x] is a complex number coefficient polynomial,
is stated as the following concept.
![]() is
computed via
Euclidean Algorithm and a relaxed
termination criterion which should be imposed at a given accuracy level
is
computed via
Euclidean Algorithm and a relaxed
termination criterion which should be imposed at a given accuracy level ![]() .
The
algorithm to compute
.
The
algorithm to compute ![]() -GCD of f1 and f2 is summarized as follows:
-GCD of f1 and f2 is summarized as follows: