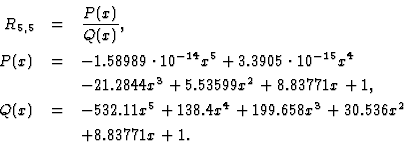Next: Summary
Up: Accuracy Analysis of Hybrid
Previous: Accuracy of HRFA
We show how the error of HRFA satisfies the error estimate
(11).
As a practical example, a data set
is considered and approximated by HRFA with the accuracy level
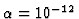 .
.
The data set D
is obtained by discretization of a function
f(x)=1/(1+25x2).
Because of the presence of a roundoff error,
rational interpolation of D is obtained by linearized equations such as
The leading and the second coefficients of P(x) is smaller
than 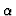 .
Thus deg
(P(x))=3.
Since
.
Thus deg
(P(x))=3.
Since
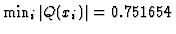 ,
we put c=1.33041.
Thus, the accuracy of symbolic-numeric hybrid rational interpolation is
,
we put c=1.33041.
Thus, the accuracy of symbolic-numeric hybrid rational interpolation is
near-GCD(P,Q) with
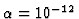 is obtained as
is obtained as
Thus rational function is obtained by (8) as
The expression can be replaced by
The result satisfies the theorem 4.1.
IMACS ACA'98 Electronic Proceedings