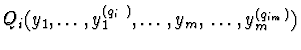 and
Rj=
and
Rj=
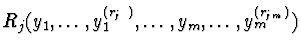 are polynomial functions with
coefficients in the differential ring R for all
are polynomial functions with
coefficients in the differential ring R for all
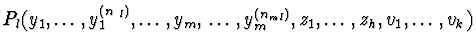 in
in
Let zi=
exp(Qi) and let vj=
log(Rj), where
Qi=
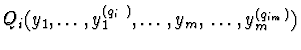 and
Rj=
and
Rj=
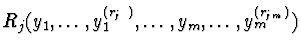 are polynomial functions with
coefficients in the differential ring R for all
are polynomial functions with
coefficients in the differential ring R for all
![]() and
all
and
all
![]() ,
e.g.
,
e.g.
![]() for all
i and j.
The system of ordinary differential equations
for all
i and j.
The system of ordinary differential equations
is in general a system of nonlinear and nonalgebraic differential equations.={ Pl=
=0,
}
Since exp(a) (respectively log(a)) with a in a differential ring Rare uniquely defined by the differential equations
{
y(1)-a(1)y=0 } (respectively
{
ay(1)-a(1)=0 }) up to a constant, then the system ![]() is equivalent to the system
is equivalent to the system
where P(ml) is the derivative of order ml of Pl for all={ Pl=
=0, Pl(1)=0,..., Pl(ml)=0, zi= exp(Qi), vj= log(Rj), zi(1)=
Qi(1)zi, Rjvj(1)= Rj(1),
,
,
},
Let N=max{ntl,qit,rjt:
![]() ,
,
![]() ,
,
![]() ,
,
![]() }. By using results from section 3, the
system
}. By using results from section 3, the
system ![]() is equivalent to the system
is equivalent to the system
={ Pl=
=0, zi(1)= Qi(1)zi, Rjvj(1)= Rj(1), P1l1=
=0,..., Pklk=
=0,..., P(k+h)lk+h=
=0, zi= exp(Qi), vj= log(Rj),
,
,
,
,
},
Let z=exp(p). The system={
=0,
=0}.
By eliminating z the system is equivalent to tha system={ p(1)-z-1=0, q(1)+qz-1=0, z-exp(p)=0, z(1)-p(1)z=0}.
is the solution of the system, where c, c1 are arbitrary constants.={ p(1)-z-1=0, q(1)+qz-1=0, p(2)-(p(1))2+p(1)=0, z-exp(p)=0, z(1)-p(1)z=0}.
,
),