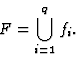 |
(2) |
Following M. Barnsley [2], under fractals we mean compact subsets of a complete metric space.
A deterministic Iterated Function System (IFS)
[2] is a structure
| F = ((X,d), f1, f2, ..., fN), | (1) |
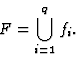 |
(2) |
The metric space
![]() ,
with Hausdorff metric
h, is also complete. When functions fi are contractions,
the IFS is hyperbolic. In this case, there is a compact
subset AF of X which is the fixed point of the operator F:
,
with Hausdorff metric
h, is also complete. When functions fi are contractions,
the IFS is hyperbolic. In this case, there is a compact
subset AF of X which is the fixed point of the operator F:
| (3) |
Such a set is called the attractor of the IFS F. The pair
![]() is a set dynamical system whose attractive
point is a set (rather than a point) - the attractor AF.
Realizing the dynamics of such a dynamical system, we can build a
fractal set.
is a set dynamical system whose attractive
point is a set (rather than a point) - the attractor AF.
Realizing the dynamics of such a dynamical system, we can build a
fractal set.
The Hausdorff metric is defined as follows:
| (4) |
where
We are dealing here with hyperbolic IFSs with all fi affine transformations.