We can conveniently work in the unit square
![]()
![]() for the
space X. The IFS under consideration is
appropriately scaled to fit into S.
for the
space X. The IFS under consideration is
appropriately scaled to fit into S.
In practice, we are dealing with approximations of fractals
rather than with fractals themselves.
We work not in the space X but in its pixel representation
![]() and, therefore, we deal not with
and, therefore, we deal not with
![]() but with
but with
![]() and, correspondingly, with
and, correspondingly, with
![]() and
and ![]() .
In what follows under S, F and f we mean
.
In what follows under S, F and f we mean ![]() ,
,
![]() and
and ![]() ,
respectively.
,
respectively.
One way to build a fractal [4], specified by IFS,
looks as follows. We take an initial
![]() and
define
and
define
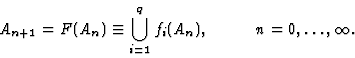 |
(5) |
| (6) |
Barnsley's deterministic algorithm [2] for building a
fractal implies the calculation of each ![]() for every point
for every point
![]() ,
,
![]() for every iteration. When we
wish to rebuild the fractal, we have to repeat the whole above
procedure.
for every iteration. When we
wish to rebuild the fractal, we have to repeat the whole above
procedure.