Conclusions

Using massless $\varphi ^4$ theory as an example, we have shown that a uniform expansion of solutions for quasilinear Klein-Gordon equations can be constructed even in the main resonance case. To construct the uniform expansion we have used the Poincare-Lindstedt method and the nontrivial zero approximation: the function

$$\varphi_0^{\vphantom{+}}(x,t)= A\Bigl\{\mathop{\rm cn}\nolim... ...t),k)-\mathop{\rm cn}\nolimits(\alpha (x+\omega t),k)\Bigr\},$$

with k=0.451075598811 and $\alpha=1.0576653982$.

Thus, using the Jacobi elliptic function cn instead of the trigonometric function cos, we have put the main resonance to zero and constructed with accuracy ${\cal O}(\varepsilon^3)$ the doubly periodic solution in the standing wave form:

$$\varphi(x,\omega t)=\varphi_0^{\vphantom{+}}(x,\omega t)+ \va... ...mega t)+ {\cal O}(\varepsilon^3)\mbox{, \ with the frequency }$$

$$\omega=1+\frac{\gamma^2}{64k^2}A^2 \varepsilon-\frac{\gamma^4... ...silon -0.6031974518A^4\varepsilon^2 +{\cal O}(\varepsilon^3).$$

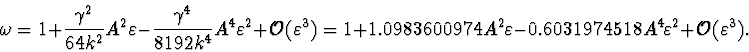
Acknowledgement

The authors are grateful to M. V. Chichikina, V. F. Edneral and P. K. Silaev for valuable discussions. S.Yu.V. would like to thank the Organizing Committee of the Fourth International IMACS Conference on Applications of Computer Algebra (ACA'98) for invitation to the Conference, hospitality and financial support.

This work has been supported by the Russian Foundation for Basic Research.