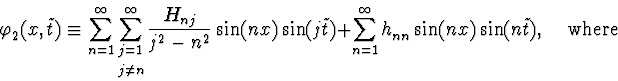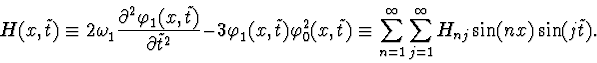Let us consider the equation to second order in
![]() :
:
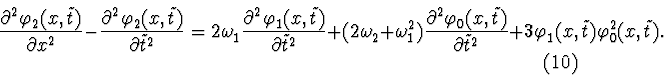
If all diagonal
coefficients of
![]() are zeros:
are zeros:
![]() :
:
![]() ,
then
,
then
![]() :
:
![]() ,
and
the function
,
and
the function
![]() has no diagonal harmonics. Hence, selecting
has no diagonal harmonics. Hence, selecting
![]() ,
we obtain a periodic solution to equation (10):
,
we obtain a periodic solution to equation (10):