Construction of asymptotic solutions via the Poincare-Lindstedt method

The purpose of this article is the construction of standing wave solutions of equation (1) with M=0, using asymptotic methods. They can only be applied provided $\varepsilon\ll 1$.

We use the Poincare-Lindstedt method: introduce the new time $\tilde t\equiv \omega t$ and seek a doubly periodic solution of equation (1) $\varphi(x,\tilde t)$ and the frequency (in time) $\omega$ in the form of power series in $\varepsilon$:

$$\begin{array}{r@{\;\equiv\;}l} \displaystyle \varphi(x,\tild... ...{n=1}^\infty\omega_n^{\vphantom{+}} \varepsilon^n. \end{array}$$

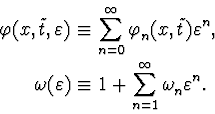
After we expand the Lagrange-Euler equation in a power series in $\varepsilon$ and obtain a sequence of equations. Write two leading equations:

1) To zero order in $\varepsilon$ the equation in $\varphi_0^{\vphantom{+}}$ is:

$$\frac{\partial^2\varphi_0^{\vphantom{+}}(x,\tilde t)}{\partia... ...^{\vphantom{+}}(x,\tilde t)} {\partial \tilde t^2}=0, \eqno(3)$$

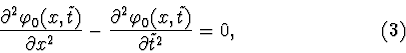
2) To first order in $\varepsilon$ the equation in $\varphi_0^{\vphantom{+}}$, $\varphi_1^{\vphantom{+}}$ and $\omega_1^{\vphantom{+}}$ is:

$$\frac{\partial^2\varphi_1^{\vphantom{+}}(x,\tilde t)}{\partia... ...de t)}{\partial \tilde t^2} +\varphi_0^3(x,\tilde t). \eqno(4)$$

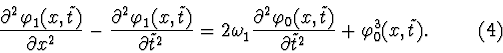
Equation (3) has many periodic solutions. If we select as a solution for this equation the function $\varphi_0^{\vphantom{+}}(x,\tilde t)=\sin(x)\sin(\tilde t)$, then the second equation hasn't periodic solutions, because the frequency of the external force $\sin(3x)\sin(3\tilde t)$is equal to the frequency of its own oscillations and it is impossible to put this resonance harmonic to zero, selecting only $\omega_1^{\vphantom{+}}$. In massless case correct selection of not only the frequency $\omega(\varepsilon)$, but also the function $\varphi_0^{\vphantom{+}}(x,\tilde t)$ allows to find a uniform expansion.