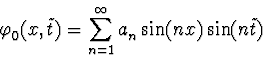
The general solution in the standing wave form (2) for equation (3) is the function
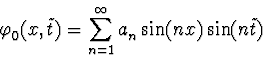
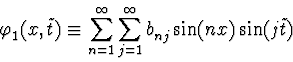
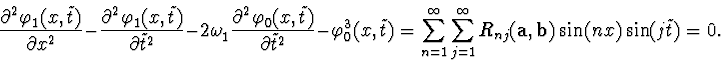
This system has a subsystem of the equations
in Fourier coefficients of the function
![]() :
:
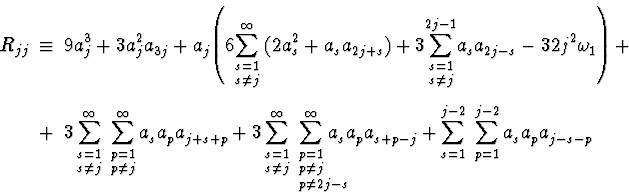
We have obtained the necessary and sufficient condition of the existence of
periodic solutions for equation (4): there exists a periodic function
![]() ,
satisfying equation (4), if and
only if the Fourier coefficients of the function
,
satisfying equation (4), if and
only if the Fourier coefficients of the function
![]() satisfy system (5).
satisfy system (5).
Coefficient
![]() is a parameter determining the
oscillation amplitude. In fact, let
is a parameter determining the
oscillation amplitude. In fact, let
![]() and
and
![]() ,
then all
polynomials
,
then all
polynomials
![]() are proportional to a13:
are proportional to a13:
![]() and, therefore, the coefficient
and, therefore, the coefficient
![]() can be selected arbitrarily.
can be selected arbitrarily.