As described in the previous section, we have obtained a set of good
specialization conditions. Each condition different from the first one, ie
that corresponding to the list
![$[0,\ldots,0]$](img132.gif) ,
is presented in the following
way:
,
is presented in the following
way:
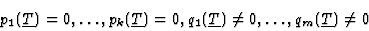 |
(3) |
where 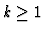 ,
,
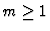 and the pi's and the qi's are polynomials in
and the pi's and the qi's are polynomials in
![${\mathchoice {\hbox{$\textstyle {\rm Z\!\!Z}$ }} {\hbox{$\textstyle
{\rm Z\!\!...
...e {\rm Z\!\!Z}$ }}
{\hbox{$\scriptscriptstyle {\rm Z\!\!Z}$ }}}[\underline{T}]$](img136.gif) non constant. In what follows it is showed how the
description of every condition can be simplified.
non constant. In what follows it is showed how the
description of every condition can be simplified.
In the case of one parameter,
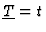 ,
if
,
if
the considered condition (3), with
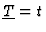 ,
is equivalent
to
,
is equivalent
to
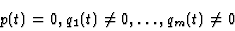 |
(4) |
If p(t)=1, ie the pi's are coprime, then this condition is directly
discarded since it would be never verified. If
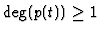 then by
defining iteratively
then by
defining iteratively
it is
easy to verify that the condition (4) is equivalent to
In the case of several parameters, it is clear that the same approach can not
be further followed but several heuristics can be adopted in order to
simplify the output:
- To check for emptyness with respect to the equalities: if the Grobner
Basis of
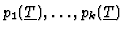 with respect to any
monomial ordering is equal to 1 then the corresponding condition is
discarded.
with respect to any
monomial ordering is equal to 1 then the corresponding condition is
discarded.
- To apply a ``lazy factorization" approach as in the GPT strategy (see
[6] or subsection 1.4).
IMACS ACA'98 Electronic Proceedings
![]() ,
if
,
if