


Next: Conclusion
Up: Solving LMI and BMI
Previous: Optimization by QE and
Algorithm 1 (Feasible problems)
``Find X which satisfies
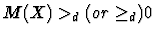 ''
''
- 1.
- Transform
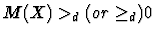 to an equivalent formula
to an equivalent formula
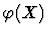 by using Sylvester's theorem.
by using Sylvester's theorem.
- 2.
- Construct the first-order formula
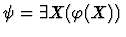 .
.
- 3.
- Perform QE for
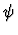 .
.
QE outputs true or false.
In the case of true QE returns one feasible solution.
false means there are no feasible solutions.
Example 1
``Does BMI
B(
x1,
x2) <
d 0 have any feasible solutions in
![$(x_1,x_2) \in [-\frac{1}{2},2]\times [-3,7]$](img57.gif)
? [
9]'' where
B(
x1,
x2)=
![$
\left [
\begin{array}{ccc}
-10 & -\frac{1}{2} & -2 \\
-\frac{1}{2} & \frac{9}...
...-\frac{1}{10} & \frac{6}{5} & -1 \\
-\frac{2}{5} & -1 & 0
\end{array}\right ]
$](img58.gif)
![$+x_2
\left [
\begin{array}{ccc}
9 & \frac{1}{2} & 0 \\
\frac{1}{2} & 0 & -3 \\...
...y}{ccc}
0 & 0 & 2 \\
0 & -\frac{11}{2} & 3 \\
2 & 3 & 0
\end{array}\right ].
$](img59.gif)
This problem is equivalent to the following QE problem:
where
A1 = -45x1+9x2+50 > 0 ,
A2 = (-4950x2-25)x12+(990x22+6590x2+4100)x1-217x22
-2020x2-4525 > 0,
A3 = (-11000x23+37500x22-102750x2+40375)x13+
(-700x23
-15850x22+141250x2-27500)x12+
(3680x23+12935x22
-71900x2-19625)x1-764x23-3280x22+7000x2+9000 > 0.
After performing QE for this, we
have ``true''.
In the case of
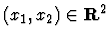 ,
after performing QE for
,
after performing QE for
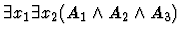 we also have true.
we also have true.
Algorithm 2 (linear objective minimization problems)
``minimize '
cT X subject to
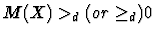
.
- 1.
- Transform
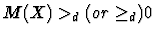 to an equivalent formula
to an equivalent formula
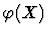 by using Sylvester's theorem.
by using Sylvester's theorem.
- 2.
- Assign the new variable z to the objective function;
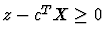 .
.
- 3.
- Construct the first-order formula
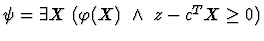 .
.
- 4.
- Perform QE for
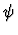 .
.
We consider some examples (which are modified one taken
from [20]), and apply the above mentioned method
to them in order to demonstrate the potential of QE approach
to SDP problems.
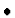 Non-Parametric: Minimize x1+x2 subject to
Non-Parametric: Minimize x1+x2 subject to
![\begin{displaymath}
\left [
\begin{array}{ccc}
1 & x_1 & 0 \\
x_1 & x_2 & 0 \\
0 & 0 & x_1+1
\end{array}\right] \geq_d 0.
\end{displaymath}](img66.gif) |
(8) |
The semidefinite constraint (8) is reduced to
a Boolean system of inequalities constraints by using
Sylvester's criterion;
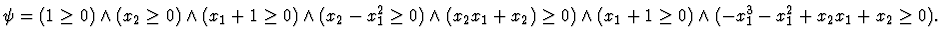
Assign new slack variable z to objective function x1+x2 and let
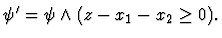 Then the problem is formulated as a first-order formula
Then the problem is formulated as a first-order formula
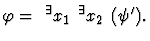 After QE we have an equivalent qf formula describing
the range of objective function;
After QE we have an equivalent qf formula describing
the range of objective function;
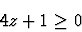 |
(9) |
 Parametric(1): Minimize ax1+x2 subject to (8)
with a parameter a.
Parametric(1): Minimize ax1+x2 subject to (8)
with a parameter a.
Let
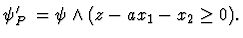 The problem is formulated as
The problem is formulated as
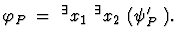 After QE we have an equivalent qf formula
describing
the range of objective function z with a parameter a;
After QE we have an equivalent qf formula
describing
the range of objective function z with a parameter a;
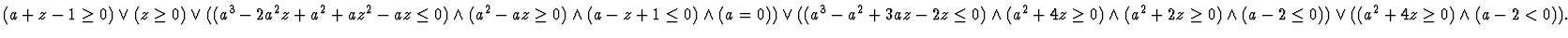
If we substitute a parameter a with 1 and simplify the result,
we have same result as
(9).
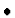 Restricted region:
Minimize x1+x2 subject to (8)
in restricted domains D1,D2 respectively,
where
(i)
Restricted region:
Minimize x1+x2 subject to (8)
in restricted domains D1,D2 respectively,
where
(i)
 and
(ii)
and
(ii)
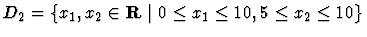 .
.
(i) In this case the problem is formulated as
After QE we have
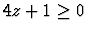 .
.
(ii) In this case the problem is formulated as
After QE we have
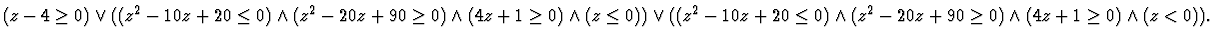
 Parametric(2): Minimize x1+x2 subject to
Parametric(2): Minimize x1+x2 subject to
![\begin{displaymath}
\left [
\begin{array}{ccc}
s & x_1 & 0 \\
x_1 & x_2 & 0 \\
0 & 0 & x_1+1
\end{array}\right] \geq_d 0.
\end{displaymath}](img80.gif) |
(10) |
where s is a parameter.
The semidefinite constraint (10) is reduced to
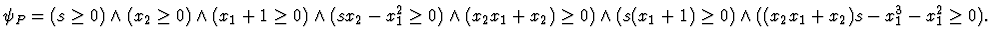
Let
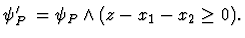 Then the problem is formulated as a first-order formula
Then the problem is formulated as a first-order formula
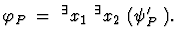 After QE we obtain
After QE we obtain
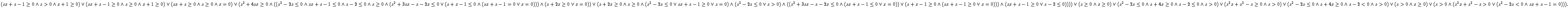
If we substitute the parameter s with 1
and simplify the result, we have same result as
(9).
 Parameter uncertainty:
Minimize x1+x2 subject to (10)
within the regions of a parameter s (i)
Parameter uncertainty:
Minimize x1+x2 subject to (10)
within the regions of a parameter s (i)
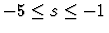 ,
(ii)
,
(ii)
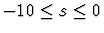 , respectively.
, respectively.
For (i),(ii), the problem is formulated as a first-order formula;
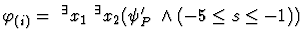 ,
,
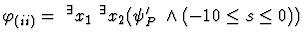 ,
respectively.
After QE we obtain ``false'' for (i) and for (ii)
,
respectively.
After QE we obtain ``false'' for (i) and for (ii)
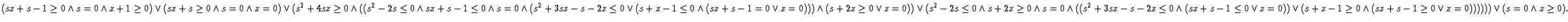



Next: Conclusion
Up: Solving LMI and BMI
Previous: Optimization by QE and
IMACS ACA'98 Electronic Proceedings
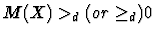 to an equivalent formula
to an equivalent formula
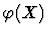 by using Sylvester's theorem.
by using Sylvester's theorem.
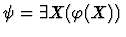 .
.
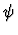 .
.
![$
\left [
\begin{array}{ccc}
-10 & -\frac{1}{2} & -2 \\
-\frac{1}{2} & \frac{9}...
...-\frac{1}{10} & \frac{6}{5} & -1 \\
-\frac{2}{5} & -1 & 0
\end{array}\right ]
$](img58.gif)
![$+x_2
\left [
\begin{array}{ccc}
9 & \frac{1}{2} & 0 \\
\frac{1}{2} & 0 & -3 \\...
...y}{ccc}
0 & 0 & 2 \\
0 & -\frac{11}{2} & 3 \\
2 & 3 & 0
\end{array}\right ].
$](img59.gif)
![\begin{displaymath}
\left [
\begin{array}{ccc}
1 & x_1 & 0 \\
x_1 & x_2 & 0 \\
0 & 0 & x_1+1
\end{array}\right] \geq_d 0.
\end{displaymath}](img66.gif)
![\begin{displaymath}
\left [
\begin{array}{ccc}
s & x_1 & 0 \\
x_1 & x_2 & 0 \\
0 & 0 & x_1+1
\end{array}\right] \geq_d 0.
\end{displaymath}](img80.gif)