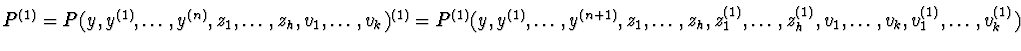 and let J1 be the ideal (P, P(1),
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
and let J1 be the ideal (P, P(1),
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
![$R[y,\ldots,y^{(N)},
y^{(N+1)},z_{1},\ldots,z_{h},z_{1}^{(1)},\ldots,z_{h}^{(1)},v_{1},\ldots,v_{k},
v_{1}^{(1)},\\ \ldots,v_{k}^{(1)}]$](img63.gif) .
.
Let
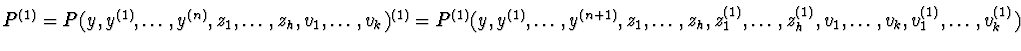 and let J1 be the ideal (P, P(1),
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
and let J1 be the ideal (P, P(1),
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
![]() ,
,
![]() )
in the polynomial ring
)
in the polynomial ring
![$R[y,\ldots,y^{(N)},
y^{(N+1)},z_{1},\ldots,z_{h},z_{1}^{(1)},\ldots,z_{h}^{(1)},v_{1},\ldots,v_{k},
v_{1}^{(1)},\\ \ldots,v_{k}^{(1)}]$](img63.gif) .
.
Let
![]() be the lexicographic term ordering on the set of power
products in
be the lexicographic term ordering on the set of power
products in
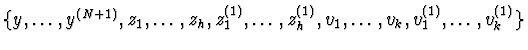 ,
with
,
with
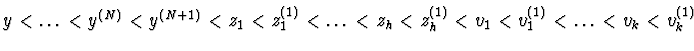 .
.
Let G1 be the reduced Gröbner basis of the ideal J1 with respect
to
![]()
[Buchberger (1976),Buchberger (1976)]. Since P(1)=
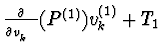 and
Rkvk(1)-Rk(1) have degree one in
vk(1), then
P and S1=
and
Rkvk(1)-Rk(1) have degree one in
vk(1), then
P and S1=
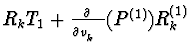 are in
are in
![$J_{1} \cap R[y,\ldots,y^{(N+1)},z_{1},\ldots,
z_{h},z_{1}^{(1)},\ldots,z_{h}^{(1)},v_{1},\ldots,v_{k},v_{1}^{(1)},
\ldots,v_{k-1}^{(1)}]$](img69.gif) .
So it is possible to eliminate
vk(1)between P(1) and
Rkvk(1)-Rk(1) and by using equalities
zi(1)=Qi(1)zi a polynomial
P1'=
.
So it is possible to eliminate
vk(1)between P(1) and
Rkvk(1)-Rk(1) and by using equalities
zi(1)=Qi(1)zi a polynomial
P1'=
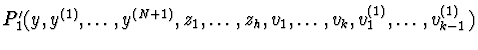 is obtained with
is obtained with
![]() .
.
If vk does not appear in P1', then P1' is in
![$J_{1} \cap R[y,\ldots,y^{(N+1)},z_{1},\ldots,z_{h},\\
v_{1},\ldots,v_{k-1},v_{1}^{(1)},\ldots,v_{k-1}^{(1)}]$](img72.gif) .
If vk appears in P1', then
.
If vk appears in P1', then
![]() and the resultant of P and
P1' with respect to the variable vk is in
and the resultant of P and
P1' with respect to the variable vk is in
![$J_{1} \cap F[y,\ldots,y^{(N+1)},z_{1},\ldots,z_{h},z_{1}^{(1)},
\ldots,z_{h}^{(1)},v_{1},\ldots,v_{k-1},v_{1}^{(1)},\ldots,v_{k-1}^{(1)}]$](img74.gif) .
So there exists at least one differential polynomial P1 in
.
So there exists at least one differential polynomial P1 in
![$G_{1} \cap F[y,\ldots,y^{(N+1)},z_{1},\ldots,\\ z_{h},z_{1}^{(1)},
\ldots,z_{h}^{(1)},v_{1},\ldots,v_{k-1},v_{1}^{(1)},\ldots,v_{k-1}^{(1)}]$](img75.gif) by definition of Gröbner basis
by definition of Gröbner basis
with respect to a lexicographic
term ordering.
Let G11=
![$G_{1} \cap R[y,\ldots,y^{(N+1)},z_{1},\ldots,z_{h},z_{1}^{(1)},
\ldots,z_{h}^{(1)},v_{1},\ldots,v_{k-1},v_{1}^{(1)},\\ \ldots,v_{k-1}^{(1)}]$](img76.gif) .
Since G11 is the reduced Gröbner basis of
J11=
.
Since G11 is the reduced Gröbner basis of
J11=
![$J_{1} \cap R[y,\ldots,y^{(N+1)},\\ z_{1},\ldots,z_{h},z_{1}^{(1)},
\ldots,z_{h}^{(1)},v_{1},\ldots,v_{k-1},v_{1}^{(1)},\ldots,v_{k-1}^{(1)}]$](img77.gif) with respect to
with respect to
![]() and
and
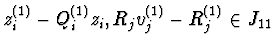 for all
for all
![]() ,
,
![]() ,
then
,
then
![]() and P1=
and P1=
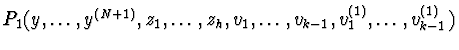 .
If
degvk-1(1)P1=d, then
the pseudoremainder P1* of P1 with respect to
Rk-1vk-1(1)-Rk-1(1) as polynomials in
vk-1(1) is
in J11 and
vk-1(1) does not appear in P1*. So we can
assume that P1=
.
If
degvk-1(1)P1=d, then
the pseudoremainder P1* of P1 with respect to
Rk-1vk-1(1)-Rk-1(1) as polynomials in
vk-1(1) is
in J11 and
vk-1(1) does not appear in P1*. So we can
assume that P1=
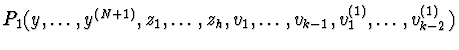 .
.
(i) By using the Ritt process of differential
reduction for the extended characteristic set, it is sufficient to find
the extended characteristic set of the differential polynomials Pand
Rkvk(1)-Rk(1). It riquires the
pseudo division of P(1) by
Rkvk(1)-Rk(1) as
polynomials in
![$R[y,\ldots,y^{(N+1)},z_{1},\ldots,z_{h},z_{1}^{(1)},
\ldots,\\ z_{h}^{(1)},v_{1},\ldots,v_{k},v_{1}^{(1)},\ldots,v_{k-1}^{(1)}]
[v_{k}^{(1)}]$](img83.gif) and the extended characteristic set of the partial remainder
of the above pseudodivision R1 and P [Ritt (1950].
and the extended characteristic set of the partial remainder
of the above pseudodivision R1 and P [Ritt (1950].
(ii) By using the differential resultant theory, e.g. by finding the
differential resultant of the differential polynomials P and
Rkvk(1)-Rk(1), as differential polynomials in
![]() .
By differential
resultant theory such differential resultant is equal to the resultant of
the polynomials P, P(1) and
Rkvk(1)-Rk(1) in the
polynomial ring
.
By differential
resultant theory such differential resultant is equal to the resultant of
the polynomials P, P(1) and
Rkvk(1)-Rk(1) in the
polynomial ring
![$R[y,\ldots,y^{(N+1)},z_{1},\ldots,z_{h},z_{1}^{(1)},\\
\ldots,z_{h}^{(1)},v_{1},\ldots,v_{k-1},v_{1}^{(1)},\ldots,v_{k-1}^{(1)}]
[v_{k},v_{k}^{(1)}]$](img85.gif) [Carra' Ferro (1997)].
[Carra' Ferro (1997)].
In all such elimination procedures of one differential variable the differential
polynomials P, P(1) and
Rkvk(1)-Rk(1) are involved.
(iii) By using the differential Gröbner basis theory with respect to
an elimination differential term ordering [Carra' Ferro (1987),Ollivier (1990)]
[Weispfenning (1993)].