


Next: An Elimination Procedure of
Up: Nonalgebraic Ordinary Differential Equations
Previous: Nonalgebraic Ordinary Differential Equations
Let R be a differential ring and let 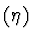 be the following system of
ordinary algebraic differential equations:
be the following system of
ordinary algebraic differential equations:
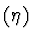
={
P=
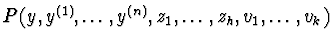
=0,
zi(1)-
Qi(1)zi=0,
Rjvj(1)-
Rj(1)=0,
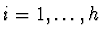
,
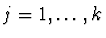
}.
with
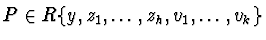 ,
,
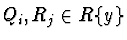 ,
ord(Qi)=qi and
,
ord(Qi)=qi and
ord(Rj)=rj for
all i and j.
First of all in the following subsubsection an elimination procedure of one
differential variable will be shown.
IMACS ACA'98 Electronic Proceedings