Rjvj(1)-Rj(1)=0,
Let N=max{n,qi,rj:
![]() ,
,
![]() }.
}.
By using an elimination procedure of the variable vk the system ![]() becomes
equivalent to the system
becomes
equivalent to the system
with={ P=0, P(1)=0, P1=0, zi(1)-Qi(1)zi=0,
Rjvj(1)-Rj(1)=0,,
}.
By using an elimination procedure of the variable vk-1 the system
![]() becomes equivalent to the system
becomes equivalent to the system
with={ P=0, P(1)=0, P1=0, P1(1)=0, P2=0, zi(1)-Qi(1)zi=0,
Rjvj(1)-Rj(1)=0,,
}.
Finally by using recursively an elimination procedure of the variables
![]() the system
the system ![]() is
equivalent to the system
is
equivalent to the system
with={ P=0, P(1)=0, P1=0, P1(1)=0, ..., Pk=0, Pk(1)=0,..., Pk+i-1=0, Pk+i-1(1)=0, Pk+i=0, zi(1)-Qi(1)zi=0, Rjvj(1)-Rj(1)=0,
,
}.
If i=h, then the system ![]() is equivalent to the system
is equivalent to the system
with={ P=0, P(1)=0, P1=0, P1(1)=0, ..., Pk=0, Pk(1)=0,..., Pk+h-1=0, Pk+h-1(1)=0, Pk+h=0, zi(1)-Qi(1)zi=0, Rjvj(1)-Rj(1)=0,
,
}.
Now the differential ideal I=[P,
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
![]() ,
,
![]() ]=
[P, P1=0,..., Pk,...,Pk+h-1, Pk+h=0,
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
]=
[P, P1=0,..., Pk,...,Pk+h-1, Pk+h=0,
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
![]() ,
,
![]() ]
so the systems
]
so the systems ![]() and
and ![]() are
equivalent.
are
equivalent.
Let ![]() be the following system
be the following system
The system={ P=0, P(1)=0, P1=0, P1(1)=0, ..., Pk=0, Pk(1)=0,...,
Pk+h-1=0, Pk+h-1(1)=0, Pk+h=0, zi= exp(Qi), vj= log(Rj),
zi(1)-Qi(1)zi=0, Rjvj(1)-Rj(1)=0,,
}.
Since each elimination of one variable among zi and vj riquires
one more derivative of P by 3.1.1., then
![]() and
the system
and
the system ![]() is equivalent to the following system
is equivalent to the following system ![]() :
:
={ P=0, P(1)=0,..., P(h+k)=0, zi= exp(Qi), vj= log(Rj),
zi(1)-Qi(1)zi=0, Rjvj(1)-Rj(1)=0,,
}.
Finally the differential equation {
![]() } is equivalent to the system
} is equivalent to the system
={ P=
=0, Ph+k=
= 0, zi= exp(Qi), vj= log(Rj),
,
, },
(i) By using the Ritt's theory of characteristic sets it is sufficient to
find the unique differential polynomial
![]() in the extended
characteristic set of the set of differential polynomials
in the extended
characteristic set of the set of differential polynomials
![]() P, zi(1)-Qi(1)zi, Rjvj(1)-Rj(1):
P, zi(1)-Qi(1)zi, Rjvj(1)-Rj(1):
![]() ,
,
![]() ,
,
![]()
![]() with respect to
a ranking O of the differential variables, such that
with respect to
a ranking O of the differential variables, such that
![]() .
.
(ii) By using the Gröbner bases techniques, it is sufficient to find the
Gröbner basis G of the ideal Jh+k=(
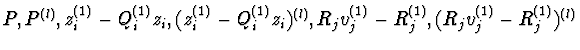 :
:
![]() ,
,
![]() ,
,
![]() )
in
)
in
![$R[y,\ldots,y^{(N+h+k)},z_{1},\ldots,z_{1}^{(h+k)},\ldots,z_{h},\ldots,
z_{h}^{(h+k)},v_{1},\ldots,v_{1}^{(h+k)},\ldots,v_{k},\ldots,\\ v_{k}^{(h+k)}]$](img108.gif) with respect to the lexicographic term ordering
with respect to the lexicographic term ordering ![]() with
with
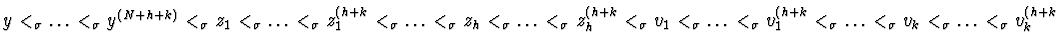 .
The riquired differential polynomial Ph+k is in
.
The riquired differential polynomial Ph+k is in
![]() .
.
(iii) By using the differential resultant theory, e.g. by finding the
differential resultant of the h+k+1 differential polynomials P,
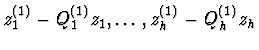 ,
,
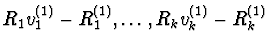 ,
as
differential polynomials in
,
as
differential polynomials in
![]() .
.
Since ord(P)=n,
ord(Qi)=qi and
ord(Rj)=rj for all i and j, let N*=
![]() .
By
differential resultant theory such differential resultant is equal to
the resultant of the polynomials P,...,
.
By
differential resultant theory such differential resultant is equal to
the resultant of the polynomials P,...,
P(N*-ord(P)),
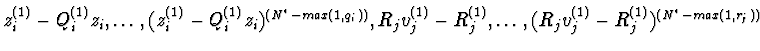 ,
,
![]() ,
,
![]() )
in the polynomial ring R[
)
in the polynomial ring R[
![$y,\ldots,y^{(N^{*})},z_{i},\ldots,
z_{i}^{(N^{*}-max(1,q_{i}))},v_{j},\ldots,v_{j}^{(N^{*}-max(1,r_{j}))}]$](img117.gif) :
:
![]() ,
,
![]() ].
].
Since each elimination process of the above differential variables riquires
at most h+k derivatives of P,
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1), then this elimination process holds also
when
![]() for some
for some
![]() .
.