This system of equations is very difficult to solve. On the one hand, all
Rjj are infinite series and the number of equations is infinite too.
On the other hand, each equation of this system is a nonlinear one. We
have restricted ourselves to finding a particular solution. To simplify
calculations we assume that the function
![]() contains only odd harmonics. Our goal is to find a
real solution and we seek
contains only odd harmonics. Our goal is to find a
real solution and we seek
![]() .
.
To find an approximate solution we apply the Galerkin method:
cut off higher diagonal harmonics
![]() :
:
![]() and seek an approximation for
and seek an approximation for
![]() in the following form
in the following form
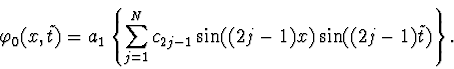
We have obtained the finite system of nonlinear equations, with the
number of equations three times as mush as that of the variables.
We solve the first N equations and substitute the obtained values in the
other equations. The system of the N leading nonlinear equations can be
solved, using standard procedures of the computer algebra system REDUCE: the SOLVE operator and the Groebner basis package [15,16].
The SOLVE operator (in "on rounded" mode) round off numbers with accuracy
![]() (the system (5) is too difficult to be solved in "off
rounded" mode).
We admit that the
system of the first N equations is solved if for all
(the system (5) is too difficult to be solved in "off
rounded" mode).
We admit that the
system of the first N equations is solved if for all ![]() the
inequalities
the
inequalities
![]() are true. We also admit that
the value of N is sufficient to solve system (5) if for all
are true. We also admit that
the value of N is sufficient to solve system (5) if for all
![]() the inequalities
the inequalities
![]() are true.
are true.
Using the SOLVE operator and computer with 128M bytes
operating memory (RAM) we have solved the system (5) only for N<5, but
due to a short program (see Appendix) we have found a particular solution for
any N<50 and obtained that the minimal sufficient value of N for
![]() is N=8 and that the value of the frequency is
is N=8 and that the value of the frequency is
We also have found
numerical values of the fifteen leading Fourier coefficients of
![]() .
The obtained values of
.
The obtained values of
![]() are very close to the values of the corresponding
terms of the following finite sequence:
are very close to the values of the corresponding
terms of the following finite sequence:
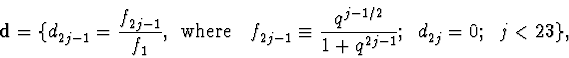
In other words, the finite sequence ![]() is an approximate solution of system (5).
These numerical calculations help to find the analytical form of
is an approximate solution of system (5).
These numerical calculations help to find the analytical form of
![]() .
The following
table illustrates this interesting result:
.
The following
table illustrates this interesting result:
|
|
|
|
|
|
1 |
1 | 0 |
|
0 |
3 |
|
|
|
|
5 |
|
|
|
|
7 |
|
|
|
|
9 |
|
|
|
|
11 |
|
|
|
|
13 |
|
|
|
|
15 |
|
|
|
|
17 |
0 |
|
|
|
19 |
0 |
|
|
|
21 |
0 |
|
|
|
23 |
0 |
|
|
|
25 |
0 |
|
|
|
27 |
0 |
|
|
|
29 |
0 |
|
|
|
31 |
0 |
|
|
|
33 |
0 |
|
|
|
35 |
0 |
|
|
|
37 |
0 |
|
|
|
39 |
0 |
|
|
|
41 |
0 |
|
|
|
43 |
0 |
|
|
|
45 |
0 |
|
|
|
| 47 | 0 | 0 | 0 |
|