The aim of this section is to find the analytical form of the function, which
Fourier coefficients satisfy system (5).
For arbitrary ![]() let us define the following
sequence:
let us define the following
sequence:
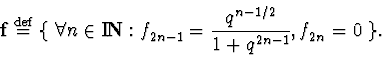
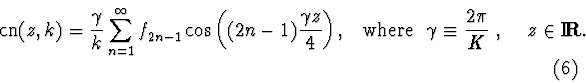
Let us clarify introduced notations and point out some properties of the elliptic cosine:
1) Basic periods of the doubly periodic function
![]() are 4K(k) and
are 4K(k) and
![]() ,
where K(k) is a full elliptic
integral,
,
where K(k) is a full elliptic
integral,
![]() and
and
![]() .
.
2) The parameter q in the Fourier expansion
can be expressed in terms of elliptic integrals:
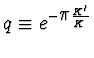 .
.
3) The Fourier-series expansion of the function
![]() does
not include even harmonics. This expansion is valid in the following
domain of the complex plane:
does
not include even harmonics. This expansion is valid in the following
domain of the complex plane:
![]() ,
in particular, for
,
in particular, for
![]() .
.
4) If
![]() and
and ![]() ,
then
,
then
![]() .
.
5) The function
![]() is a solution of the following
differential equation:
is a solution of the following
differential equation:
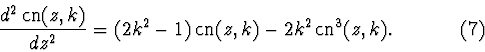
The latest property means that the infinite sequence of the Fourier
coefficients for
![]() is a solution of some infinite system of
nonlinear algebraic equations. Let us find this system.
is a solution of some infinite system of
nonlinear algebraic equations. Let us find this system.
On the one hand, it is clear from (6) that the
Fourier-series expansion for the function
![]() is:
is:
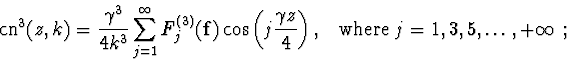
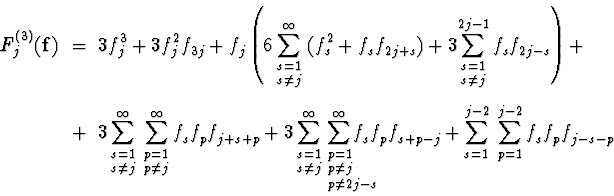
On the other hand, from the differential equation (7) it follows that
 is proportional to
is proportional to
![]() ,
with
coefficients of proportionality depending on j:
,
with
coefficients of proportionality depending on j:
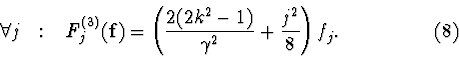
Thus, the sequence ![]() is a nonzero
solution of system (8) at all
is a nonzero
solution of system (8) at all ![]() .
The following
lemma proves the existence of a preferred value of q.
.
The following
lemma proves the existence of a preferred value of q.
![]()
| Lemma. | There exists such value of parameter
|
|---|---|
| Proof. | Inserting the
sequence |
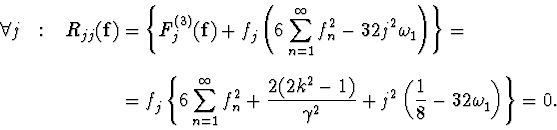
System (5) has a nonzero solution if and only if
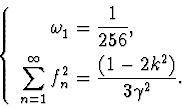
We have obtained the value of
![]() .
The second
equation of this system is equivalent to the following equation in
parameter q:
.
The second
equation of this system is equivalent to the following equation in
parameter q:
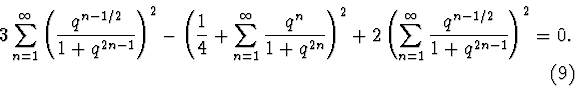
This equation has the following solution on interval (0,1):
Thus the lemma is proved.
Now it is easy to construct the required zero approximation for the
function
![]() :
:
For arbitrary ![]() this function
is a real solution of equation (4). If
this function
is a real solution of equation (4). If
![]() ,
then the periods
of
,
then the periods
of
![]() in x and in
in x and in ![]() are
equal to
are
equal to ![]() .
Using the Fourier-series expansion for the function
.
Using the Fourier-series expansion for the function
![]() (formula (6)), we obtain the following expansion for
function
(formula (6)), we obtain the following expansion for
function
![]() :
:
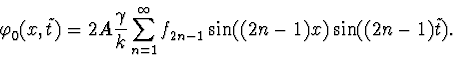
If
![]() ,
then q is a
solution of equation (9) and the sequence
,
then q is a
solution of equation (9) and the sequence ![]() is a real solution
of system (5). The middle value of q corresponds to
k=0.451075598811,
is a real solution
of system (5). The middle value of q corresponds to
k=0.451075598811,
![]() and
and
![]() .
All
equation in system (5) are homogeneous ones, hence, for these values of
parameters, the sequence of the Fourier
coefficients of the function
.
All
equation in system (5) are homogeneous ones, hence, for these values of
parameters, the sequence of the Fourier
coefficients of the function
![]() also
is a solution of system (5), with
also
is a solution of system (5), with
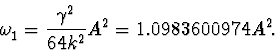
Thus we have proved that the function