Now it is easy to find this periodic
solution
![]() .
Let us designate
the Fourier coefficients of the function
.
Let us designate
the Fourier coefficients of the function
![]() as
Dnj:
as
Dnj:
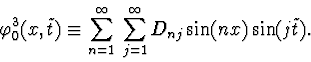
Equation (4) gives the following result(
![]() are arbitrary numbers):
are arbitrary numbers):
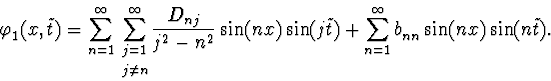
It should be noted that the function
![]() with arbitrary diagonal coefficients
with arbitrary diagonal coefficients
![]() is a
solution of equation (4) and that all off-diagonal coefficients of
is a
solution of equation (4) and that all off-diagonal coefficients of
![]() are proportional to A3.
are proportional to A3.