Computing a set of good specialization parameter conditions.
Let J be a homogeneous ideal in
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img27.gif) ,
,
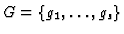 its Gröbner
basis with respect to a block
its Gröbner
basis with respect to a block
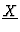 -degree-compatible ordering
-degree-compatible ordering
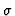 in
in
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img27.gif) .
Every polynomial gj has the structure
.
Every polynomial gj has the structure
with
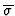 the restriction of
the restriction of 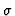 to
to
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{X}]$](img96.gif) .
For a list of s nonnegative integers
.
For a list of s nonnegative integers
![$L=[n_1,\ldots,n_s]$](img110.gif) with
with
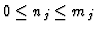 ,
the specialization condition defined by L is given by
,
the specialization condition defined by L is given by
By using corollary 1, it is clear that, for any
specialization verifying the conditions indicated by L, if the Hilbert
Function of the monomial ideal generated by
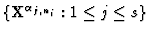 agrees with the Hilbert Function of
the monomial ideal generated by
agrees with the Hilbert Function of
the monomial ideal generated by
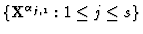 then the specialization of G is a
Gröbner Basis of the specialization of J (with respect to
then the specialization of G is a
Gröbner Basis of the specialization of J (with respect to
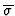 ).
This consequence of corollary 1 provides a nice way of
computing a set of conditions which are good for specializing
the Gröbner Basis of J already computed in
).
This consequence of corollary 1 provides a nice way of
computing a set of conditions which are good for specializing
the Gröbner Basis of J already computed in
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img27.gif) :
i.e. those whose Hilbert function computed
with the leading terms already present agrees with the ``generic" Hilbert
function. In order to avoid the consideration of all the possible cases
(
:
i.e. those whose Hilbert function computed
with the leading terms already present agrees with the ``generic" Hilbert
function. In order to avoid the consideration of all the possible cases
(
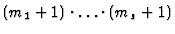 )
the following lemma and its remarks show how to know in
advance that such a condition list is bad once one such list has been
previously classified as bad.
)
the following lemma and its remarks show how to know in
advance that such a condition list is bad once one such list has been
previously classified as bad.
Lemma 1
Let
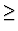
be the ordering introduced in the set of conditions lists for
G defined by
If
L is a condition list for
G bad for specialization then every
condition list
L' for
G with
L<
L' is also bad for specialization

First, it is clear that the list
![${\bf0}=[0,\ldots,0]$](img119.gif) provides a good
specialization condition. Next, it is analyzed the case of the vanishing
of some
provides a good
specialization condition. Next, it is analyzed the case of the vanishing
of some
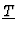 -coefficients into only one gj polynomial: for
every
-coefficients into only one gj polynomial: for
every
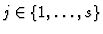 the biggest (for
the biggest (for 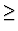 )
conditions lists for
G with only one non zero element which are good for specialization. Once
these lists have been determined, we know, by the previous lemma that we
do not need to consider any conditions list for G strictly bigger than
one of such lists. Proceeding in a similar way with the case of only two,
three, etc non-zero elements and with conditions lists not strictly
bigger than those already located in the previous step, we exhaust all the
possibilities.
)
conditions lists for
G with only one non zero element which are good for specialization. Once
these lists have been determined, we know, by the previous lemma that we
do not need to consider any conditions list for G strictly bigger than
one of such lists. Proceeding in a similar way with the case of only two,
three, etc non-zero elements and with conditions lists not strictly
bigger than those already located in the previous step, we exhaust all the
possibilities.
Graphically this means that, for this Gröbner Basis,
if we consider the set 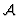 of all lists
of all lists
![$[n_1,\ldots,n_s]$](img123.gif) with
with
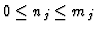 (the different specialization conditions), we are looking for
the maximal elements of the subset:
(the different specialization conditions), we are looking for
the maximal elements of the subset:
with respect to the order relation 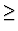 in
in 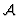 defined in Lemma
1. If
defined in Lemma
1. If
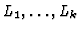 are these maximal elements of
are these maximal elements of 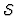 we have obtained that if, for some i,
we have obtained that if, for some i,
![$L=[n_1,\ldots,n_s]\leq L_i$](img127.gif) then the
verification of the conditions
then the
verification of the conditions
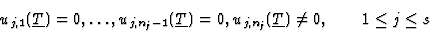 |
(2) |
implies that the specialization of the considered Gröbner Basis G gives a
Gröbner Basis of the specialized ideal.
In conclusion, every maximal element
![$L_i=[k_1,\ldots,k_s]$](img128.gif) of
of 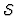 provides a set of
provides a set of
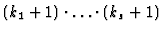 conditions with each one
having the structure showed in 2. This procedure, as it has
been explained taking only into account the set
conditions with each one
having the structure showed in 2. This procedure, as it has
been explained taking only into account the set 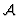 ,
can be
easily optimized if we take also into account the structure of the polynomials
,
can be
easily optimized if we take also into account the structure of the polynomials
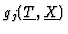 's: for example, if it is known that the
coefficient
's: for example, if it is known that the
coefficient
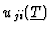 is a non zero constant then we can
discard directly from the set
is a non zero constant then we can
discard directly from the set  those lists whose j-th element is
bigger than i.
those lists whose j-th element is
bigger than i.
IMACS ACA'98 Electronic Proceedings
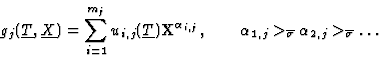
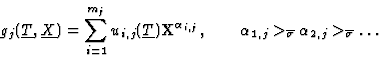

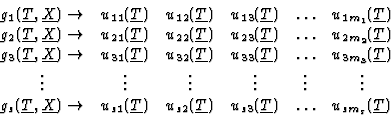
![]() of
of ![]() provides a set of
provides a set of
![]() conditions with each one
having the structure showed in 2. This procedure, as it has
been explained taking only into account the set
conditions with each one
having the structure showed in 2. This procedure, as it has
been explained taking only into account the set ![]() ,
can be
easily optimized if we take also into account the structure of the polynomials
,
can be
easily optimized if we take also into account the structure of the polynomials
![]() 's: for example, if it is known that the
coefficient
's: for example, if it is known that the
coefficient
![]() is a non zero constant then we can
discard directly from the set
is a non zero constant then we can
discard directly from the set ![]() those lists whose j-th element is
bigger than i.
those lists whose j-th element is
bigger than i.