Corollary 1
Let
J be a homogeneous ideal in
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img27.gif)
,
G its Gröbner basis with respect to
a block
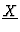
-degree-compatible ordering
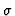
in
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img27.gif)
and

the specialization map giving
values to the parameters in
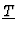
.
Let
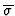
be
the restriction of
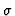
to
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{X}]$](img96.gif)
,

the Hilbert function of the ideal
generated by the
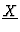
-leading power products of
G and

the Hilbert function of the ideal
generated by the leading power products of

.
If
then

is a Gröbner basis of

with respect to
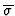
.
