Linear-armed robot design problem

Figure 7 shows the construction of a linear-armed robot consisting of a battery, a DC motor and a ball thread. In Figure 7, f_o and v_o are the output force and velocity of the robot hand respectively.

  

Figure 7: Construction of a linear-armed robot

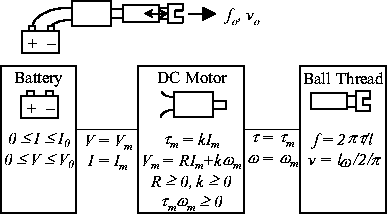
Sets of constraints holding these components are given as below.

• Battery

  $0 \leq I \leq I_{0},\; 0 \leq V \leq V_{0}.$

  I: output current
  I₀: upper limit of output current
  V: output voltage
  V₀: upper limit of output voltage

• DC motor

  $\tau_{m}=kI_{m},\; V_{m}=RI_{m}+k\omega_{m},\; R \geq 0,\; k \geq 0,\; \tau_{m}\omega_{m} \geq 0.$

  $\tau_{m}$: output torque
  $\omega_{m}$: output angular velocity
  I_m: input current
  V_m: input voltage
  k: torque constant
  R: resistance

• Ball thread

  $f=2\pi\tau/l,\; v=l\omega/2/\pi.$

  f: output force
  v: output velocity
  $\omega$: input angular velocity
  l: lead

Battery's output voltage and current are the same as DC motor's input voltage and current, and DC motor's output torque and angular velocity are the same as ball thread's input torque and angular velocity. Furthermore, ball thread's output force and velocity are identical with the output force and velocity of the robot hand. Therefore, whole the constraints holding the linear-armed robot are given as Eq. (8).

$$\begin{array}{l} 0 \leq I \leq I_{0},\; 0 \leq V \leq V_{0},... ...pi\tau/l,\; v=l\omega/2/\pi,\\ f_{o}=f,\; v_{o}=v. \end{array}$$ (8)

Let Eq. (9) be the given requirement to the linear-armed robot.

$$f_{o} > 90 \mbox{[N]}.$$ (9)

In this problem, the designer has to determine variable values satisfying Eq. (8) and (9). In actual design, the designer does not design a battery, a DC motor or a ball thread. Instead, commercial components are used. Firstly, they are roughly selected based on the size or the weight. After that, their performance are checked in detail and the acceptable components are used. In this example, for simplicity, it is assumed that the following components are used.

Battery:

$I_{0}=1\mbox{[A]},\; V_{0}=9\mbox{[V]}.$

DC motor:

$k=0.02\mbox{[Nm/A]},\; R=2\mbox{[$\Omega$ ]}.$

Ball thread:

$l/2/\pi=1.6\times 10^{-4}\mbox{[m]}.$

Suppose that the designer likes to determine the output velocity of the robot hand and gives a constraint `` $v_{o} > 0.07\mbox{[m/s]}$'' to the algebraic under constraint solver. Then, all the inequalities are transformed into a form of equation by introducing slack variables, the reduction tree is constructed, and inconsistency is found among the following constraints.

$$f_{o} > 90,\; v_{o} > 0.07,\; V \leq V_{0},\; V_{0} = 9\;, R = 2, k = 0.02, l/2/\pi=1.6 \times 10^{-4}.$$

The designer may relax the constraint about the output velocity v_o and replace the constraint `` $v_{o} > 0.07\mbox{[m/s]}$'' by a new one `` $v_{o}>0.06\mbox{[m/s]}$''. Then, any inconsistency is found at the symbolic part of the algebraic under constraint solver, and the following numerical solution is computed by the numeric part.

$$\begin{array}{l} f_{o}=f=90.05\mbox{[N]},\; v_{o}=v=6.005\tim... ... = 8.947\mbox{[V]},\; I_{m} = I = 0.7204\mbox{[A]}. \end{array}$$