Gearbox layout problem

Figure 8 shows a three-axes gearbox. This section shows an example of the gear axes layout problem to determine the positions of gear axes for given gear diameters and size of the box.

  

Figure 8: Three-axes gearbox

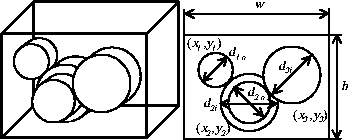
Each variable in Figure 8 shows:

• $(x_{j},y_{j})\;(j=1,2,3)$: position of the jth axis
• $d_{ji},d_{jo}\;(j=1,2,3)$: diameter of the input and output gear of the jth axis
• w,h: width and height of the gearbox

The constraints holding the problem are given as below.

$$\begin{array}{l} (x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=((d_{1o... ... w-d_{3i}/2,\; d_{3i}/2 \leq y_{3} \leq h-d_{3i}/2. \end{array}$$ (10)

In Eq. (10), the first equation shows meshing between the first axis and the second axis gear. The second equation shows meshing between the second axis and the third axis gear. The third shows no meshing between the first axis and the third axis gear. The rest of Eq. (10) is the condition that all the gears are in the gearbox.

Let Eq. (11) be the given gear diameters.

$$d_{1o}=42\mbox{[mm]},d_{2i}=86\mbox{[mm]},d_{2o}=70\mbox{[mm]},d_{3i}=110\mbox{[mm]}.$$ (11)

Suppose the following gearboxes are given.

1.

$w=180\mbox{[mm]},h=180\mbox{[mm]}.$

The constraint set is firstly received by the symbolic part and inconsistency is not found. After removing redundant constraints, numerical solutions are computed by the numeric part. The following example solution is obtained.

(x₁,y₁,x₂,y₂,x₃,y₃) = (97.4,54.2,43,87.9,125,125)

2.

$w=160\mbox{[mm]},h=160\mbox{[mm]}.$

The constraint set is firstly received by the symbolic part and inconsistency is not found. After removing redundant constraints, numerical solutions are computed by the numeric part. However, no numerical solution is obtained and it concluded that there exists no solution which satisfies the given constraints.