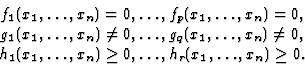Reduction tree

Let Eq. (1) be the constraint set defined at the conceptual design stage.

$$\begin{array}{c} f_{1}(x_{1},\ldots,x_{n})=0,\ldots,f_{p}(x_... ...n}) \geq 0,\ldots,h_{r}(x_{1},\ldots,x_{n}) \geq 0. \end{array}$$ (1)

By introducing slack variables s_j and t_k, Eq. (1) is transformed to Eq. (2) and (3).

$$\begin{array}{c} f_{1}(x_{1},\ldots,x_{n})=0,\ldots,f_{p}(x_... ..._{n})=t_{1},\ldots,h_{r}(x_{1},\ldots,x_{n})=t_{r}. \end{array}$$ (2)

$$t_{1} \geq 0,\ldots,t_{r} \geq 0.$$ (3)

A set of Eq. (2) and (3) is equivalent to Eq. (1). The symbolic part computes equations consisting of $(t_{1},\ldots,t_{r})$ from Eq. (2), and finds out inconsistencies and new constraints according to the following criteria.

Criteria of inconsistency

1.

If all the coefficients of a polynomial consisting of $(t_{1},\ldots,t_{r})$ are positive and it is equal to a negative constant, there exists inconsistency.
For example, if `` t<sub>1</sub> + t<sub>2</sub>t<sub>3</sub> = -3'' is computed, there exists inconsistency among `` $h_{1}(x_{1},\ldots,x_{n})\geq 0$'', `` $h_{2}(x_{1},\ldots,x_{n})\geq 0$'' and `` $h_{3}(x_{1},\ldots,x_{n})\geq 0$''.

2.

If all the coefficients of a polynomial consisting of $(t_{1},\ldots,t_{r})$ are positive and it is equal to zero, a new constraint is obtained.
For example, if `` t<sub>1</sub> + t<sub>2</sub>t<sub>3</sub> = 0'' is computed, a new constraint `` $h_{1}(x_{1},\ldots,x_{n}) = 0 \land \{h_{2}(x_{1},\ldots,x_{n}) = 0 \lor h_{3}(x_{1},\ldots,x_{n}) = 0\}$'' is obtained.

$\Box$

Figure 2 shows the geometrical meaning of this method of checking inconsistency. By introducing slack variables s and t, the surface defined by Eq. (1) in x-space is transformed to the surface defined by Eq. (2) and (3) in $(\mbox{\boldmath$x,s,t$ })$-space. The condition that there exists inconsistency in Eq. (2) and (3) means that the surface defined by Eq. (2) does not pass through the region defined by Eq. (3). Thus, by projecting the surface defined by Eq. (2) in $(\mbox{\boldmath$x,s,t$ })$-space to t-space, the inconsistency in Eq. (2) and Eq. (3) can be checked.

  

Figure 2: Geometric meaning of the inconsistency checking

Polynomials consisting of $(t_{1},\ldots,t_{r})$ are computed by constructing a reduction tree. At the initial state, a reduction tree is a tree whose nodes are Eq. (2). After that, each equation is regarded as a reduction rule which reduces [2] other equations, and new nodes are generated by applying the reduction rules according to the following procedures. In reduction, the slack variables t are given the lexicographically lower rank than any other variable. Figure 3 shows an example of a reduction tree.

Procedures of constructing a reduction tree

1.

  The slack variables t are given the lexicographically lower rank than any other variable. Let C and $C^{\prime}$ be $\{f_{i}(\mbox{\boldmath$x$ })=0,g_{j}(\mbox{\boldmath$x$ })\cdot s_{j}=1,h_{k}(\mbox{\boldmath$x$ })=t_{k}\;(1\leq i\leq p,1\leq j\leq q,1\leq k\leq r)\}$ and $\emptyset$ respectively. Then, a tree whose leaf nodes are equations in C is constructed.

2.

  An equation held at each node of the reduction tree is reduced by each equation in C only once. If more than one equation in C can reduce the equation at the node, all of them are applied. Then, child nodes which hold the new equations generated by reduction are added to the node. If no equation in C can reduce the equation, it is appended to $C^{\prime}$.

3.

  If an equation consisting of t is generated, it is checked by the criteria described above. If inconsistency or a new constraint is found, the computation is finished.

4.

  If there is a new node added to the reduction tree, go back to Step 2.

5.

  If $C^{\prime}$ is empty, the computation is finished. Otherwise, let C be $C \cup C^{\prime}$ and go back to Step 2.

$\Box$

  

Figure 3: Reduction tree

In order to efficiently find out inconsistency, the symbolic part uses the following heuristics.

Heuristics improving computational efficiency

1.

Decreasing the number of generated nodes

If an equation held at a node can be reduced by several equations in C whose head terms are prime to each other, only one equation of them is applied and only one child node is generated.

In order to improve computational efficiency, it should be avoided to generate same equations. This heuristics is based on the fact that the normal form [2] of an equation obtained by applying equations whose head terms are prime to each other is identical irrespective of the order of using these equations.

2.

Ordering between variables and normalizing the equation set

Variables appearing in an inequality are given the lowest rank next to the slack variables t, and the equation set is normalized by computing its Gröbner base.

A constraint interact with another constraint which has common variables. Figure 4 shows a constraint graph [1,3] which visually represents interrelationships between constraints. A constraint graph is defined as a bipartite graph whose nodes are classified into two groups: variable nodes and constraint nodes. A variable node is connected with constraint nodes in which the variable appears. Reductions are conducted between two constraint nodes connected with the common variable nodes. Thus, it is considered that if distances between inequality constraint nodes are short then equations consisting of t are efficiently obtained. This heuristics has an effect of transforming a constraint graph into the new one which has shorter distances between inequality constraint nodes.

  

Figure 4: Constraint graph and its transformation

$\Box$