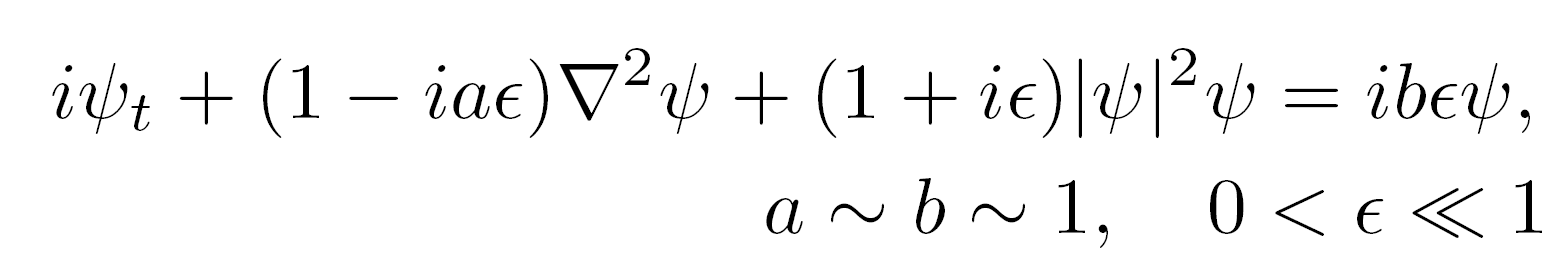
Supported by NSF grant DMS 0807131
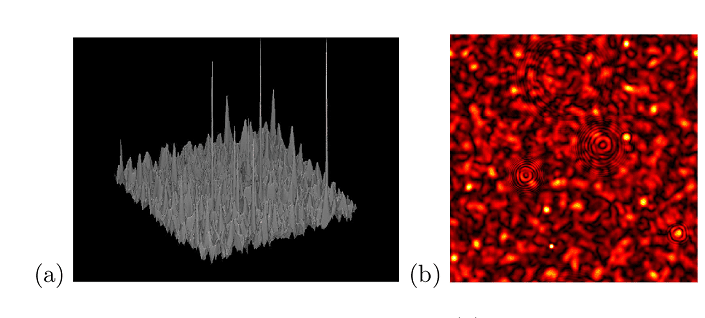
(a)Snapshot of absolute value of psi vs. spatial coordinates (x,y). (b)Snapshot of density plot for psi shows collapse decay with emission of cylindrical waves.
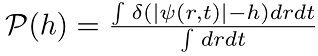
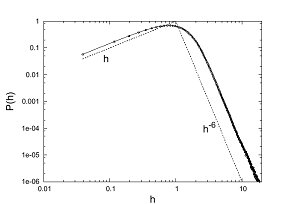
shows algebraic tails due to collapses:
| Pavel M. Lushnikov: |
Researh interests |
|
| Video of Skoltech Colloquium | Popular Lecture on singularities and wavebreaking (in Russian) |
|
Strong turbulence in critical 2D nonlinear Schrodinger equation
Supported by NSF grant DMS 0807131
|

(a)Snapshot of absolute value of psi vs. spatial coordinates (x,y). (b)Snapshot of density plot for psi shows collapse decay with emission of cylindrical waves. |
Probability distribution function
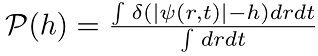
shows algebraic tails due to collapses: |
 |
|
Microscopic vs. macroscopic dynamics of biological cells due to contact interaction and chemotaxis
|
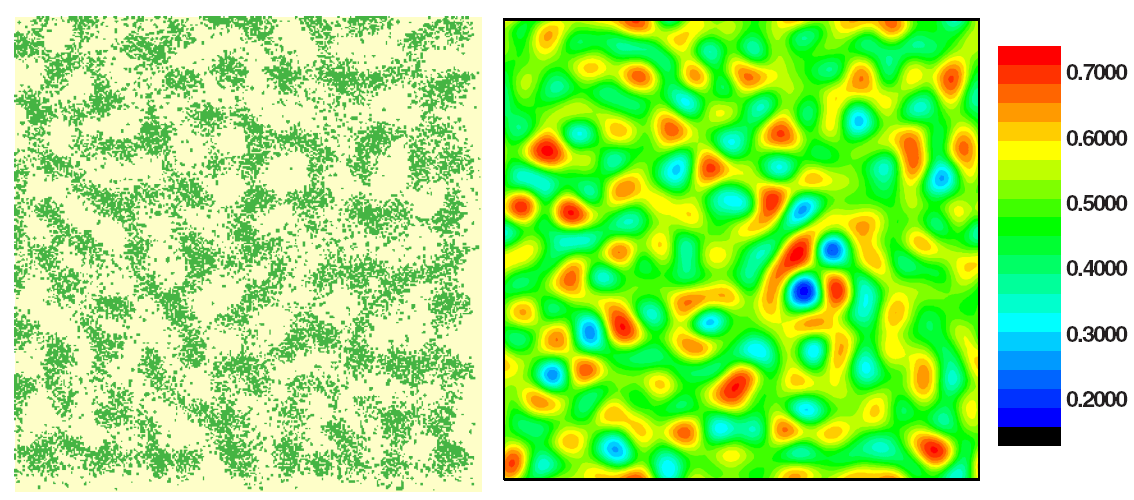
Simulation of early vascular network formation. Left: Microsopic Monte Carlo simulation of dynamics of 15 000 cells. Each cell has fluctuating shape. Right: simualtion of cellular density in macrosopic model. Scale bar represent volume fraction of cells. |
|
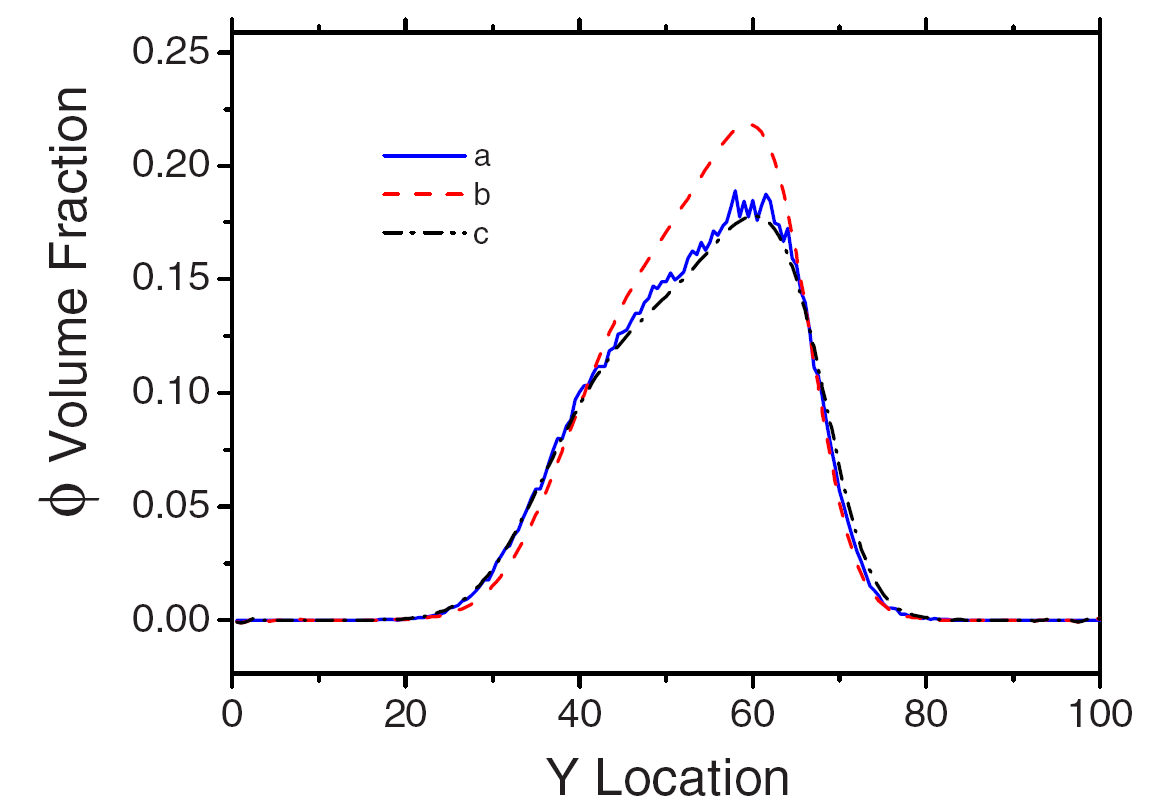
Cross sections of the volume fraction in 2D for (a) Monte Carlo microscopic simulation, (b) Keller-Segel macroscopic model
(no contact cell-cellinteractions) and (c) Macroscopic nonlinear diffusion equation coupled with chemotaxis:
|
 |
Laser fusion and laser-plasma interactions
|
 |
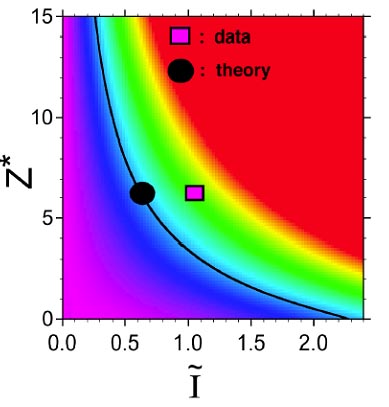 |
Dispersion-managed soliton in
optical fiber communications
|
Nonlinear Schrodinger equation for dispersion-managed optical fiber system:
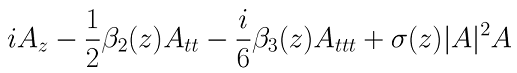
|
|
Oscillating tails of dispersion-managed soliton.
Curve 1: numerical simulation. Curve 2: analytical prediction: |
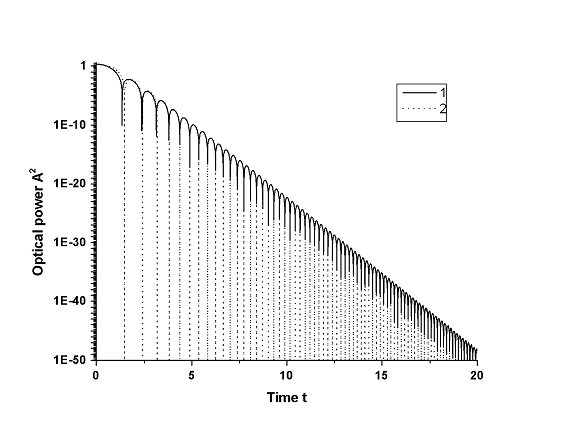
|
|
Link to Pavel Lushnikov's web page at the University of New Mexico Last modified: 02/03/2009. |