


Next: An Elimination Procedure
Up: Systems of Nonlinear and
Previous: Differential Algebra Preliminaries
Let
P=
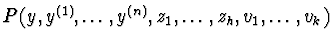 be a polynomial in the variables
be a polynomial in the variables
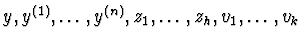 with
coefficients in a differential ring R of functions. So
with
coefficients in a differential ring R of functions. So
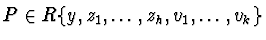 .
.
Let zi=
exp(Qi) and let vj=
log(Rj), where
Qi=
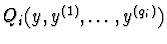 and
Rj=
and
Rj=
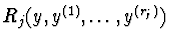 are polynomial functions with
coefficients in the
are polynomial functions with
coefficients in the
differential ring R for all
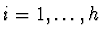 and
all
and
all
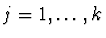 ,
e.g.
,
e.g.
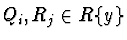 for all i and j.
Moreover
ord(Qi)=qi and
ord(Rj)=rj for all i and j.
for all i and j.
Moreover
ord(Qi)=qi and
ord(Rj)=rj for all i and j.
The ordinary differential equation
is in general nonlinear and nonalgebraic.
Since exp(a) (respectively log(a)) with a in a differential ring Rare uniquely defined by the differential equations
{
y(1)-a(1)y=0 } (respectively
{
ay(1)-a(1)=0 }) up to a constant, then the equation
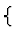 P=0
P=0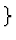 is equivalent to the system
is equivalent to the system
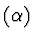 ={ P=
={ P=
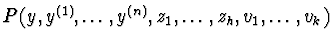 =0, P(1)=0,..., P(m)=0,
zi=
exp(Qi), vj=
log(Rj),
zi(1)=
Qi(1)exp(Qi)=
Qi(1)zi,
=0, P(1)=0,..., P(m)=0,
zi=
exp(Qi), vj=
log(Rj),
zi(1)=
Qi(1)exp(Qi)=
Qi(1)zi,
Rjvj(1)=
Rj(1),
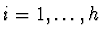 ,
,
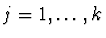 ,
,
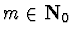 },
},
where P(m) is the derivative of order m of P for all 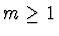 .
.
EXAMPLE 2
Let
P=P(y,y(1),y(2),exp(Q1),exp(Q2),log(R1)=
yy(2)-exp(y+(y(1))2)log(y+y(3))y(1)-(exp(y-y(2)))2y2
(y(1))3,
where
Q1=
y+(
y(1))
2,
Q2=
y-
y(2)and
R1=
y+
y(3).
If
z1=
exp(
Q1),
z2=
exp(
Q2) and
v1=
log(
R1), then
P=yy(2)-z1v1y(1)-z22y2(y(1))3.
The equation { P=0 } is equivalent to the system
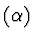
={
P=
yy(2)-
z1v1y(1)-
z22y2(
y(1))
3=0,
P(1)=0,...,
P(m)=0,
z1=
exp(
y+(
y(1))
2),
z2=
exp(
y-
y(2)))
2),
v1=
log(
y+
y(3)),
z1(1)=
(
y(1)+2
y(1)y(2))
z1,
z2(1)=
(
y(1)-
y(3))
z2,
(
y+
y(3))
v1(1)=
y(1)+
y(4),
}.
Let 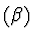 be the following system of algebraic differential equations
be the following system of algebraic differential equations
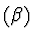 ={ P=
={ P=
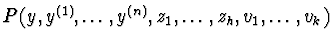 =0, P(1)=0,..., P(m)=0,
zi(1)=
Qi(1)zi,
Rjvj(1)=
Rj(1),
=0, P(1)=0,..., P(m)=0,
zi(1)=
Qi(1)zi,
Rjvj(1)=
Rj(1),
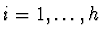 ,
,
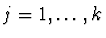 ,
,
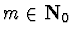 },
},
with
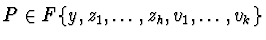 ,
,
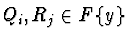 for all i and j.
for all i and j.
It is possible to find a system 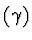 of algebraic ordinary differential
equations in the same differential variables
of algebraic ordinary differential
equations in the same differential variables
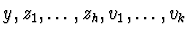 ,
that is equivalent to
,
that is equivalent to 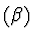 ,
such that it contains
a differential polynomial equation in the differential variable y. In other
words we can find a different set of differential generators of the
differential ideal I=[P,
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
,
such that it contains
a differential polynomial equation in the differential variable y. In other
words we can find a different set of differential generators of the
differential ideal I=[P,
zi(1)-Qi(1)zi,
Rjvj(1)-Rj(1),
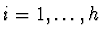 ,
,
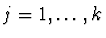 ], that has
the riquired properties.
], that has
the riquired properties.



Next: An Elimination Procedure
Up: Systems of Nonlinear and
Previous: Differential Algebra Preliminaries
IMACS ACA'98 Electronic Proceedings
![]() be a polynomial in the variables
be a polynomial in the variables
![]() with
coefficients in a differential ring R of functions. So
with
coefficients in a differential ring R of functions. So
![]() .
.
![]() and
Rj=
and
Rj=
![]() are polynomial functions with
coefficients in the
are polynomial functions with
coefficients in the ![]() and
all
and
all
![]() ,
e.g.
,
e.g.
![]() for all i and j.
Moreover
ord(Qi)=qi and
ord(Rj)=rj for all i and j.
for all i and j.
Moreover
ord(Qi)=qi and
ord(Rj)=rj for all i and j.
![]() P=0
P=0![]() is equivalent to the system
is equivalent to the system
={ P=
=0, P(1)=0,..., P(m)=0, zi= exp(Qi), vj= log(Rj), zi(1)= Qi(1)exp(Qi)= Qi(1)zi,
,
,
},
![]() be the following system of algebraic differential equations
be the following system of algebraic differential equations
={ P=
=0, P(1)=0,..., P(m)=0, zi(1)= Qi(1)zi, Rjvj(1)= Rj(1),
,
,
},