This section is devoted to present the state of the art in this kind of
techniques. Let
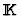 be a field and
be a field and
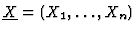 ,
,
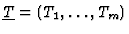 sets of variables. We call specialization any ring homomorphism
sets of variables. We call specialization any ring homomorphism
![$\varphi:{\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]\rightarrow {\rm I\kern -2.2pt K\hskip 1pt}[\underline{X}]$](img20.gif) such that
such that
![$\varphi({\rm I\kern -2.2pt K\hskip 1pt}[\underline{T}])={\rm I\kern -2.2pt K\hskip 1pt}$](img21.gif) and
and
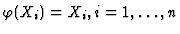 .
The
specialization associated to a point
.
The
specialization associated to a point
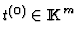 is the one defined by
is the one defined by
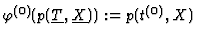 ,
for
,
for
![$p(\underline{T},\underline{X})\in{\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img25.gif) .
Let
.
Let
![$I=<F_1(\underline{T},\underline{X}),\dots,F_m(\underline{T},
\underline{X})>\subseteq
{\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img26.gif) be an ideal,
> a monomial ordering in
be an ideal,
> a monomial ordering in
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img27.gif) and
and
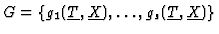 a Gröbner basis of I with respect to
>.
The most practical question that we would like to solve is to determine the
subset W of
a Gröbner basis of I with respect to
>.
The most practical question that we would like to solve is to determine the
subset W of
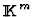 such that
such that
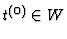 if and only if its associated
specialization
if and only if its associated
specialization
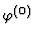 verifies that
verifies that
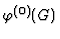 is a
Gröbner basis of
is a
Gröbner basis of
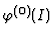 .
From a computational point of view
this is the most interesting aspect, as once we have computed W, every
time that we are given a value to the parameters we just have to test if
it belongs or not to W to determine if we have or not a Gröbner basis.
There are two possibilities to deal with this problem: to perform the initial
Gröbner Bases computation in
.
From a computational point of view
this is the most interesting aspect, as once we have computed W, every
time that we are given a value to the parameters we just have to test if
it belongs or not to W to determine if we have or not a Gröbner basis.
There are two possibilities to deal with this problem: to perform the initial
Gröbner Bases computation in
![${\rm I\kern -2.2pt K\hskip 1pt}(\underline{T})[\underline{X}]$](img34.gif) or in
or in
![${\rm I\kern -2.2pt K\hskip 1pt}[\underline{T},\underline{X}]$](img27.gif) .
.
IMACS ACA'98 Electronic Proceedings